
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0),点B(3,0)和点C(0,3).
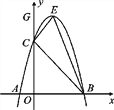
(1)求抛物线的解析式和顶点E的坐标;
(2)点C是否在以BE为直径的圆上?请说明理由;
(3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R的坐标,若不存在,请说明理由.
【答案】(1)y=-x2+2x+3,E (1,4);(2)在;(3)Q1(1,-2),R1(4,-5);
Q2(1,-8),R2(-2,-5);R3(2,3),Q3(1,0).
【解析】试题分析:(1)运用待定系数法即可得出函数关系式,然后进行配方即可得出顶点坐标;
(2)过点E分别作x轴、y轴的垂线,垂足分别F、G.易证△BCE为直角三角形,点C在以BE为直径的圆上;
(3)利用平行四边形的性质易得点Q、R的坐标.
试题解析: (1) 将A(-1,0),B(3,0)和C(0,3)代入y=ax2+bx+c
得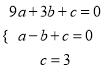
解得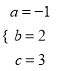
∴抛物线的解析式为y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点E的坐标为(1,4).
(2)点C在以BE为直径的圆上,理由如下:
如图,过点E分别作x轴、y轴的垂线,垂足分别F、G.
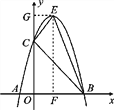
在Rt△BOC中,OB=3,OC=3,∴BC2=18
在Rt△CEG中,EG=1,CG=OG-OC=4-3=1,∴CE2=2
在Rt△BFE中,FE=4,BF=OB-OF=3-1=2, ∴BE2=20
∴BC2+CE2=BE2
故△BCE为直角三角形,点C在以BE为直径的圆上.
(3)存在,点Q、R的坐标分别为Q1(1,-2),R1(4,-5);
Q2(1,-8),R2(-2,-5);R3(2,3),Q3(1,0).


科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx+3m﹣3,以下说法:①图象过定点(![]() ),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )
),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )
A. ①② B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(1)求证:AE=BD;
(2)请判断△CMN的形状,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标中,点![]() 在第一象限内,
在第一象限内,![]() 且
且![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,
,

(1)当点![]() 的坐标为
的坐标为![]() 时(如图),求这个反比例函数的解析式;
时(如图),求这个反比例函数的解析式;
(2)当点![]() 在反比例函数
在反比例函数![]() 的图像上,且在点
的图像上,且在点![]() 的右侧时(如图2),用含字母
的右侧时(如图2),用含字母![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(3)在第(2)小题的条件下,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
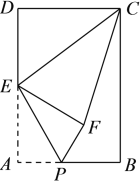
【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店出售A,B两种笔记本,其中购买2本A型笔记本和3本B型笔记本花费42元,购买3本A型笔记本和2本B型笔记本花费38元.
(1)A型笔记本和B型笔记本的单价为多少元?
(2)若一次购买B型笔记本超过20本时,超过20本部分的B型记笔记价格打8折,分别写出两种笔记本的付款金额y(元)关于购买量x(本)的函数解析式;
(3)某校准备在一次学习竞赛后购买这90本两种笔记本用于奖励,其中A型笔记本数量不超过B型笔记本的一半,两种笔记本各买多少时,总费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com