
【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
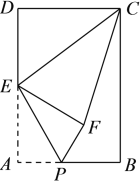
【答案】1或![]() .
.
【解析】
分∠CFE=90°和∠CEF=90°两种情况求AP得长即可.
①当∠CFE=90°时(如图所示),△ECF是直角三角形,
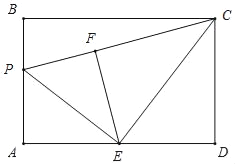
由折叠可得,∠PFE=∠A=90°,AE=FE=DE,
∴∠CFP=180°,即点P,F,C在一条直线上,
在Rt△CDE和Rt△CFE中,
![]() ,
,
∴Rt△CDE≌Rt△CFE(HL),
∴CF=CD=4,
设AP=FP=x,则BP=4﹣x,CP=x+4,
在Rt△BCP中,BP2+BC2=PC2,即(4﹣x)2+62=(x+4)2,
解得x=![]() ,即AP=
,即AP=![]() ;
;
②当∠CEF=90°时(如图所示),△ECF是直角三角形,
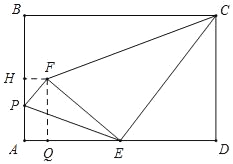
过F作FH⊥AB于H,作FQ⊥AD于Q,则∠FQE=∠D=90°,
又∵∠FEQ+∠CED=90°=∠ECD+∠CED,
∴∠FEQ=∠ECD,
∴△FEQ∽△ECD,
∴![]() ,即
,即![]() ,
,
解得FQ=![]() ,QE=
,QE=![]() ,
,
∴AQ=HF=![]() ,AH=
,AH=![]() ,
,
设AP=FP=x,则HP=![]() ﹣x,
﹣x,
∵Rt△PFH中,HP2+HF2=PF2,即(![]() ﹣x)2+(
﹣x)2+(![]() )2=x2,
)2=x2,
解得x=1,即AP=1.
综上所述,AP的长为1或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的袋子中装有2个白球和1个红球,这些球除颜色不同外其余都相同,搅匀后,
(1)从中一次性摸出两只球,用树状图或列表表示其中一个是红球另一个是白球的所有结果并求其概率.
(2)向袋子中放入若干个红球(与原红球相同),搅匀后,从中任取一个球是红球的概率为![]() ,求放入红球的个数.
,求放入红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0),点B(3,0)和点C(0,3).
(1)求抛物线的解析式和顶点E的坐标;
(2)点C是否在以BE为直径的圆上?请说明理由;
(3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
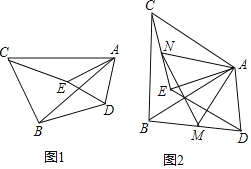
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN,若AC=6,AE=4,∠EAC=60°,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC的三个顶点的坐标分别为A(1,5),B(1,-2),C(4,0).
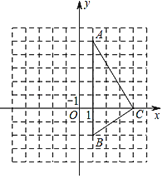
(1)请在图中画出△ABC关于y轴对称的△![]() .
.
(2)求△ABC的面积.
(3)在y轴上画出点P,使PA+PC的值最小,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com