
【题目】对于二次函数y=x2﹣2mx+3m﹣3,以下说法:①图象过定点(![]() ),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )
),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )
A. ①② B. ②③ C. ①②④ D. ①③④
【答案】C
【解析】
把x=![]() 代入即可验证①的对错;令y=0,求出的值即可判断②的对错;由函数的对称性可知,当x=0和x=2018时的函数值相等,据此求解,即可判断③的对错;先求出抛物线的对称轴,然后验证即可判断④的对错.
代入即可验证①的对错;令y=0,求出的值即可判断②的对错;由函数的对称性可知,当x=0和x=2018时的函数值相等,据此求解,即可判断③的对错;先求出抛物线的对称轴,然后验证即可判断④的对错.
①当x=![]() 时,y=
时,y=![]() ﹣2m×
﹣2m×![]() +3m﹣3=
+3m﹣3=![]() ,所以图象过定点(
,所以图象过定点(![]() ,﹣
,﹣![]() ),命题①正确;
),命题①正确;
②当y=0时,x2﹣2mx+3m﹣3=0,
△=(﹣2m)2﹣4×1×(3m﹣3)=4m2﹣12m+12=4(m﹣![]() )2+3>0,
)2+3>0,
∴函数图象与x轴一定有两个交点,
命题②正确;
③∵当x=1时的函数值与x=2017时的函数值相等,
∴当x=0和x=2018时的函数值相等,
∵当x=0时, y=x2﹣2mx+3m﹣3=3m﹣3,
∴当x=2018时,y=x2﹣2mx﹣3的函数值为﹣3,
命题③正确;
④当m=﹣1时,抛物线的解析式为:y=x2+2x﹣6,
对称轴是:x=﹣1,
设y1=﹣x+1,y2=x+3,
当x=﹣1时,y1=1+1=2,y2=﹣1+3=2,
当y=0时,x1=1,x2=﹣3,
∴直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,
命题④正确;
故选:C.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DC,BF=CE,需补充一个条件,就能使△ABE≌△DCF,小明给出以下四个答案:①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )

A.①②③④B.①②③C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.
(1)小红从甲地到乙地骑车的速度为 km/h;
(2)当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0),点B(3,0)和点C(0,3).
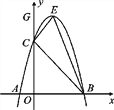
(1)求抛物线的解析式和顶点E的坐标;
(2)点C是否在以BE为直径的圆上?请说明理由;
(3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com