
分析 (1)只需比较被开方数的大小即可得出答案;
(2)先把要求的式子进行变形,再比较2+$\sqrt{3}$与3+$\sqrt{2}$的大小,最后根据两个负数比较大小,绝对值大的反而小即可得出答案.
解答 解:(1)$\root{3}{12}$<$\root{3}{13}$;
(2)∵-2-$\sqrt{3}$=-(2+$\sqrt{3}$),
-3-$\sqrt{2}$=-(3+$\sqrt{2}$),
又∵2+$\sqrt{3}$<3+$\sqrt{2}$,
∴-2-$\sqrt{3}$>-3-$\sqrt{2}$.
故答案为:<,>.
点评 此题考查了实数的大小比较,掌握实数的大小比较法则是本题的关键;注意两个无理数的比较方法:统一根据二次根式的性质,把根号外的移到根号内,只需比较被开方数的大小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
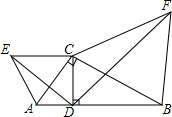 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:
设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14% | B. | 15% | C. | 16% | D. | 17% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
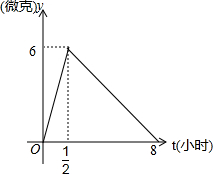 某医药研究所开发一种新药,如果承认按规定的剂量服用,据监测,服药后每毫升血液中含药量y与时间t之间关系如图所示,据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为6:00,那么服药后几点到几点有效?
某医药研究所开发一种新药,如果承认按规定的剂量服用,据监测,服药后每毫升血液中含药量y与时间t之间关系如图所示,据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为6:00,那么服药后几点到几点有效?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com