
分析 根据二次函数y=ax2+bx+c(a,b,c为常数,a≠0),顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是x=-$\frac{b}{2a}$,当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小,可得答案.
解答 解:y=-3x2+x-4化为y=a(x-h)2+k的形式为y=-3(x-$\frac{1}{6}$)2-$\frac{47}{12}$,开口向下,对称轴是x=$\frac{1}{6}$顶点坐标是($\frac{1}{6}$,-$\frac{47}{12}$),当x=$\frac{1}{6}$时,y有最大值,为-$\frac{47}{12}$,当x<$\frac{1}{6}$时,y随x增大而增大,当x>$\frac{1}{6}$时,y随x时,y随x增大而减小,抛物线与y轴交点的坐标为(0,-4),
故答案为:-3(x-$\frac{1}{6}$)2-$\frac{47}{12}$,下,x=$\frac{1}{6}$,($\frac{1}{6}$,-$\frac{47}{12}$),$\frac{1}{6}$,大,-$\frac{47}{12}$,<$\frac{1}{6}$,>$\frac{1}{6}$,(0,-4).
点评 主要考查了函数的单调性.二次函数y=ax2+bx+c(a,b,c为常数,a≠0),顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是x=-$\frac{b}{2a}$,当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
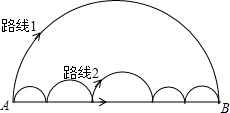 如图,有三只小虫同时出发,以相同的速度从A点到B点,甲虫沿路线1爬行,乙虫沿路线2爬行,丙虫沿直线AB爬行.则下列结论中,正确的是( )
如图,有三只小虫同时出发,以相同的速度从A点到B点,甲虫沿路线1爬行,乙虫沿路线2爬行,丙虫沿直线AB爬行.则下列结论中,正确的是( )| A. | 甲先到B点 | B. | 乙先到B点 | C. | 丙先到B点 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
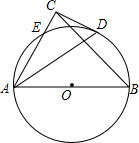 如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CE=2,CD=4.
如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CE=2,CD=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com