
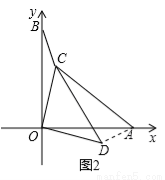
如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,-a)(a、b均大于0);
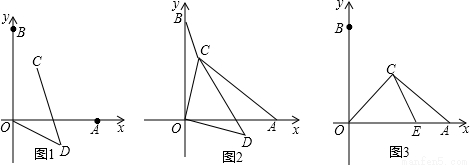
(1)连接OD、CD,求证:∠ODC=450;
(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;
(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求⊿OCA的面积。
(1)证明见解析;(2)135°;(3)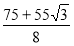 .
.
【解析】
试题分析:(1)过C点、D点向x轴、y轴作垂线,运用勾股定理计算,结合全等可证;
(2)连接DA,证△OCB≌△ODA(SAS),可得AD=CB=1,而OC=OD=2,故CD=2 ,根据勾股定理逆定理可证∠ADC=90°,易得∠OCB=∠ODA=135°;
,根据勾股定理逆定理可证∠ADC=90°,易得∠OCB=∠ODA=135°;
(3)作CF⊥OA,F为垂足,有CF2=CE2-EF2,CF2=CA2-AF2=CA2-(AE+EF)2,设EF=x,列出关于x的方程,求得x=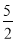 ,再在Rt△CEF中,根据勾股定理求得CF=
,再在Rt△CEF中,根据勾股定理求得CF=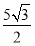 ,然后由三角形的面积公式即可求解.
,然后由三角形的面积公式即可求解.
试题解析:(1)证明:过C点、D点向x轴、y轴作垂线,垂足分别为M、N.

∵C(a,b),D(b,-a)(a、b均大于0),
∴OM=ON=a,CM=DN=b,
∴△OCM≌△ODN(SAS),
∴∠COM=∠DON.
∵∠DON+∠MOD=90°,
∴∠COM+∠MOD=90°,
∵OC=OD=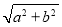 ,
,
∴△COD是等腰直角三角形,
∴∠ODC=45°;
(2)连接DA.
在△OCB与△ODA中,
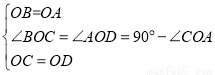 ,
,
∴△OCB≌△ODA(SAS),
∴AD=CB=1,∠OCB=∠ODA.
∵OC=OD=2,
∴CD=2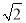 .
.
∵AD2+CD2=1+8=9,AC2=9,
∴AD2+CD2=AC2,
∴∠ADC=90°,
∴∠OCB=∠ODA=90°+45°=135°;
(3)作CF⊥OA,F为垂足,由勾股定理得
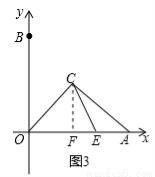
CF2=CE2-EF2,CF2=CA2-AF2=CA2-(AE+EF)2,
设EF=x,可得52-x2=72-(3+x)2,
解得x=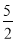 .
.
在Rt△CEF中,得CF=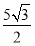 ,
,
∴OF=CF=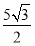 ,
,
∴△OCA的面积=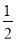 •OA•CF=
•OA•CF=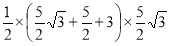 =
=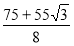 .
.
考点: 1.勾股定理;2.全等三角形的判定与性质.


科目:初中数学 来源:2015届湖南省邵阳市八年级下学期期末考试数学试卷(解析版) 题型:解答题
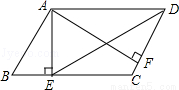
如图,在?ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=60°,BE=4,CF=2.
(1)从对称性质看,?ABCD是 _________ 对称图形;
(2)求平行四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源:2015届湖北随州府河镇中心校八年级下学期期中考试数学试卷(解析版) 题型:选择题
在四边形ABCD中,若有下列四个条件:①AB//CD;②AD=BC;③∠A=∠C;④AB=CD,现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有 ( )
(A)3组 (B)4组 (C)5组 (D)6组
查看答案和解析>>
科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:填空题
从A地向B地打长途电话,通话3分钟以内(含3分钟)收费2.4元,3分钟后每增加通话时间1分钟加收1元(不足1分钟的通话时间按1分钟计费),某人如果有12元话费打一次电话最多可以通话 分钟.
查看答案和解析>>
科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:选择题
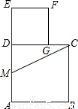
如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A.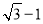 B.
B.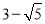 C.
C.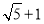 D.
D.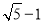
查看答案和解析>>
科目:初中数学 来源:2015届湖北省八年级3月联考数学试卷(解析版) 题型:解答题
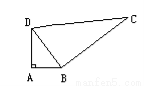
如图,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源:2015届湖北省宜昌市(城区)八年级下学期期末考试数学试卷(解析版) 题型:解答题
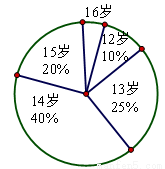
翔志学校抽样调查后得到n名学生年龄情况,将结果绘制成如下的扇形统计图。
(1)被调查学生年龄的中位数是_______岁;
(2)通过计算求该学校学生年龄的平均数(精确到1岁);
(3)被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数。
查看答案和解析>>
科目:初中数学 来源:2015届浙江省八年级4月质量检测数学试卷(解析版) 题型:选择题
数据3,1,x,-1,-3,的平均数0,则这组数的方差是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com