
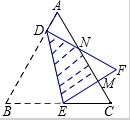
 如图,将边长为3$\sqrt{3}$+3的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=$\sqrt{3}$,则重叠部分的面积为$\frac{27+9\sqrt{3}}{4}$.
如图,将边长为3$\sqrt{3}$+3的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=$\sqrt{3}$,则重叠部分的面积为$\frac{27+9\sqrt{3}}{4}$. 分析 观察图形可知重叠部分的面积即是△DEF的面积减去△MNF的面积.由折叠的性质,可求得∠BDE=∠EDF=45°,由四边形的内角和为360°,求得∠BEF为150°,得到∠CEM为30°,则可证得∠EMC为90°;作△BDE的高,根据45°与60°的三角函数,借助于方程即可求得其高的值,则各三角形的面积可解.
解答 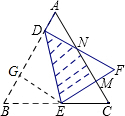 解:过点E作EG⊥AB于G,
解:过点E作EG⊥AB于G,
∴∠EGB=90°,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=3$\sqrt{3}$+3,
根据题意得:∠BDE=∠FDE,∠F=∠B=60°,
∵DF⊥AB,
∴∠FDB=90°,
∴∠BEF=360°-∠B-∠F-∠BDF=150°,∠BDE=∠FDE=$\frac{1}{2}$∠FDB=45°
∴∠MEC=180°-∠BEF=30°,
∴∠EMC=180°-∠C-∠EMC=90°,
在Rt△ADN中,AD=$\sqrt{3}$,tan∠A=tan60°=$\frac{DN}{AD}$=$\sqrt{3}$,
∴DN=3,
∴S△ADN=$\frac{1}{2}$AD•DN=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$,
在△BDE中,DB=AB-AD=3$\sqrt{3}$+3-$\sqrt{3}$=2$\sqrt{3}$+3,
∵∠EDG=45°,
∴∠DEG=45°,
∴DG=EG,
∵tan∠B=tan60°=$\frac{EG}{BG}$=$\sqrt{3}$,
设EG=x,则DG=x,BG=$\frac{\sqrt{3}}{3}$x,
∴x+$\frac{\sqrt{3}}{3}$x=3$\sqrt{3}$+3-$\sqrt{3}$=2$\sqrt{3}$+3,
解得:x=$\frac{3\sqrt{3}+3}{2}$,
∴EG=DG=$\frac{3\sqrt{3}+3}{2}$,
∴S△BDE=$\frac{1}{2}$BD•EG=$\frac{1}{2}$×(2$\sqrt{3}$+3)×$\frac{3\sqrt{3}+3}{2}$=$\frac{27+15\sqrt{3}}{4}$,
∵∠B=∠C=∠F=60°,
∴BE=$\frac{EG}{sin60°}$=3$+\sqrt{3}$,
∴EC=BC-BE=2$\sqrt{3}$,
∵∠BED=∠FED=180°-∠B-∠BDE=75°,
∴∠FNM=∠MEC=30°,
∴∠FMN=∠EMC=90°,
∴EM=EC•cos30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∴FM=EF-EM=BE-EM=$\sqrt{3}$,
∴MN=FM•tan60°=3,
∴S四边形MNDE=S△DEF-S△MNF=S△BDE-S△MNF=$\frac{27+15\sqrt{3}}{4}$-$\frac{1}{2}$×$\sqrt{3}$×3=$\frac{27+9\sqrt{3}}{4}$.
故答案为:$\frac{27+9\sqrt{3}}{4}$.
点评 本题考查了翻折变换(折叠问题),等边三角形的性质.关键是由已知推出特殊三角形,解直角三角形,由折叠的性质将线段进行转化.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com