
【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?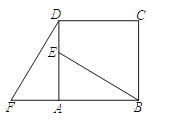
【答案】解:(1)旋转△ADF可得△ABE,
理由如下:
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠DAF=90°,
在△ADF和△ABE中,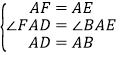 ,
,
∴△ADF≌△ABE,
∴旋转△ADF可得△ABE;
(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90°;
(3)BE=DF且BE⊥BE.理由如下:
延长BE交F于H点,如图,
∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
∵△ABE按逆时针方向旋转90°△ADF,
∴BE=DF,∠1=∠2,
∵∠3=∠4,
∴∠DHB=∠BAE=90°,
∴BE⊥DF.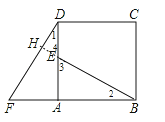
【解析】(1)旋转△ADF可得△ABE,通过证明△ADF≌△ABE即可说明问题;
(2)旋转的定义和旋转角的定义解答即可;
(3)根据旋转的性质得BE=DF,∠1=∠2,再根据三角形内角定理得到∠DHB=∠BAE=90°,所以BE⊥DF.


科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:

(1)扇形统计图中m的值为 ,n的值为 ;
(2)补全条形统计图;
(3)在选择B类的学生中,甲、乙、丙三人在乒乓球项目表现突出,现决定从这三名同学中任选两名参加市里组织的乒乓球比赛,选中甲同学的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.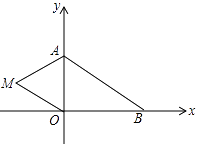
(1)a= , b=;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣ ![]() 时,在坐标轴的负半轴上求点N(的坐标),使得△ABN的面积与四边形ABOM的面积相等.(直接写出答案)
时,在坐标轴的负半轴上求点N(的坐标),使得△ABN的面积与四边形ABOM的面积相等.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出四个事件:①连续2次抛掷1枚质地均匀的硬币,2次都出现“正面朝上”;②发射一颗炮弹,命中目标;③在标准大气压下,水在1℃时结冰;④一个实心铁块丢入水中,铁块浮起,其中随机事件有_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com