练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知（x+1）（x﹣2）=x2+mx+n，则m+n=________

    【答案】-3

    【解析】

    已知等式左边利用多项式乘以多项式法则计算，再利用多项式相等的条件求出m与n的值，即可求出m+n的值．

    已知等式变形得：x2-x-2=x2+mx+n，

    可得m=-1，n=-2，

    则m+n=-1-2=-3．

    故答案为：-3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A、B的坐标分别为（3，2）、（﹣1，0），若将线段BA绕点B顺时针旋转90°得到线段BA′，则点A′的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，E是AD上任意一点，延长BA到F，使得AF=AE，连接DF：
    （1）旋转△ADF可得到哪个三角形？
    （2）旋转中心是哪一点？旋转了多少度？
    （3）BE与DF的数量关系、位置关系如何？为什么？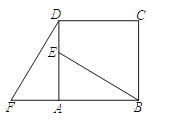

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一海轮位于灯塔P的西南方向，距离灯塔40了2海里的A处，它沿正东方向航行一段时间后，到达位于灯塔P的南偏东60°方向上的B处，求航程AB的值(结果保留根号).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点P，点Q分别代表两个小区，直线l代表两个小区中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站点．

    ①若考虑到小区P居住的老年人较多，计划建一个离小区P最近的车站，请在公路l上画出车站的位置（用点M表示）；
    ②若考虑到修路的费用问题，希望车站的位置到小区P和小区Q的距离之和最小，请在公路l上画出车站的位置（用点N表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【现场学习】
    定义：我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”．
    如：|x|=2，|2x﹣1|=3，| |﹣x=1，…都是含有绝对值的方程．
    怎样求含有绝对值的方程的解呢？基本思路是：含有绝对值的方程→不含有绝对值的方程．
    我们知道，根据绝对值的意义，由|x|=2，可得x=2或x=﹣2．
    （1）[例]解方程：|2x﹣1|=3．
    我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题．
    解：根据绝对值的意义，得2x﹣1=3或2x﹣1= ．
    解这两个一元一次方程，得x=2或x=﹣1．
    检验：
    ①当x=2时，
    原方程的左边=|2x﹣1|=|2×2﹣1|=3，
    原方程的右边=3，
    ∵左边=右边
    ∴x=2是原方程的解．
    ②当x=﹣1时，
    原方程的左边=|2x﹣1|=|2×（﹣1）﹣1|=3，
    原方程的右边=3，
    ∵左边=右边
    ∴x=﹣1是原方程的解．
    综合①②可知，原方程的解是：x=2，x=﹣1．
    【解决问题】
    解方程：| |﹣x=1．
    （2）【解决问题】解方程：| |﹣x=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】边长为7，24，25的△ABC内有一点P到三边的距离相等，则这个距离是（　　）

    A. 1.5 B. 3 C. 4 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示，则符合这一结果的实验可能是（　　）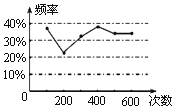

    A.掷一枚正六面体的骰子，出现5点的概率
    B.掷一枚硬币，出现正面朝上的概率
    C.任意写出一个整数，能被2整除的概率
    D.一个袋子中装着只有颜色不同，其他都相同的两个红球和一个黄球，从中任意取出一个是黄球的概率

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下给出的几何体：球、正方体、圆柱、圆锥中，主视图是矩形，俯视图是圆形的是_____．

    查看答案和解析>>

    同步练习册答案