
【题目】观察等式:![]() ;
;![]() ;
;![]() …,若设
…,若设![]() ,则用含
,则用含![]() 的式子表示
的式子表示![]() 的结果是________.
的结果是________.
【答案】![]()
【解析】
由等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2,得出规律:2+22+23+…+2n=2n+1-2,那么250+251+252+…+299+2100=(2+22+23+…+2100)-(2+22+23+…+249),将规律代入计算即可.
∵2+22=23-2;
2+22+23=24-2;
2+22+23+24=25-2;
…
∴2+22+23+…+2n=2n+1-2,
∴250+251+252+…+299+2100
=(2+22+23+…+2100)-(2+22+23+…+249)
=(2101-2)-(250-2)
=2101-250,
∵250=a,
∴2101=(250)22=![]() ,
,
∴原式=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发之后,全国许多省市对湖北各地进行了援助,广州市某医疗队备好医疗防护物资迅速援助武汉.第一批医疗队员乘坐高铁从广州出发,2.5小时后,第二批医疗队员乘坐飞机从广州出发,两批队员刚好同时到达武汉.已知广州到武汉的飞行距离为800千米,高铁路程为飞行距离的![]() 倍.
倍.
(1)求广州到武汉的高铁路程;
(2)若飞机速度与高铁速度之比为5:2,求飞机和高铁的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
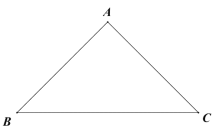
【题目】过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.
(1)如图,在等腰![]() 中,
中,![]() ,
,![]() .
.
①在下图中画出一条![]() 的形内弧;
的形内弧;
②在![]() 中,其形内弧的长度最长为______.
中,其形内弧的长度最长为______.
(2)在平面直角坐标系中,点![]() ,
,![]() ,
,![]() .点M为
.点M为![]() 形内弧所在圆的圆心.求点M纵坐标
形内弧所在圆的圆心.求点M纵坐标![]() 的取值范围;
的取值范围;
(3)在平面直角坐标系中,点![]() ,点G为x轴上一点.点P为
,点G为x轴上一点.点P为![]() 最长形内弧所在圆的圆心,求点P纵坐标
最长形内弧所在圆的圆心,求点P纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
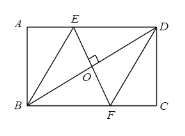
【题目】如图,在矩形ABCD中,AB=3,做BD的垂直平分线E,F,分别与AD、BC交于点E、F,连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
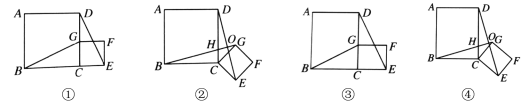
【题目】(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图④,若AB=a,BC=b;CE =ka,CG=kb,(
,如图④,若AB=a,BC=b;CE =ka,CG=kb,(![]() )试判断(1)中的结论是否仍然成立?并说明理由.
)试判断(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,以二次函数![]() 的二次项系数
的二次项系数![]() 的2倍为一次项系数,一次项系数
的2倍为一次项系数,一次项系数![]() 为常数项构造的一次函数
为常数项构造的一次函数![]() 叫做二次函数
叫做二次函数![]() 的“子函数”,反过来,二次函数
的“子函数”,反过来,二次函数![]() 叫做一次函数
叫做一次函数![]() 的“母函数”.
的“母函数”.
(1)若一次函数![]() 是二次函数
是二次函数![]() 的“子函数”,且二次函数经过点
的“子函数”,且二次函数经过点![]() ,求此二次函数的解析式.
,求此二次函数的解析式.
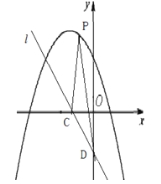
(2)如图,已知二次函数![]() 的“子函数”图象直线
的“子函数”图象直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 是直线
是直线![]() 上方的抛物线上任意一点,求
上方的抛物线上任意一点,求![]() 的面积的最大值.
的面积的最大值.
(3)已知二次函数![]() 与它的“子函数”
与它的“子函数”![]() 的函数图象有两个交点
的函数图象有两个交点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市购进一批成本为每件![]() 元的商品,经调查发现,该商品每天的销售量
元的商品,经调查发现,该商品每天的销售量![]() (件)与销售单价
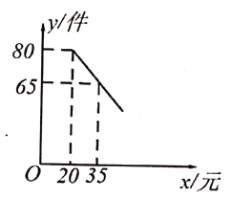
(件)与销售单价![]() (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(2)若超市按单价不低于成本价,且不高于![]() 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润
元销售,则销售单价定为多少,才能使销售该商品每天获得的利润![]() (元)最大?
(元)最大?
(3)若超市要使销售该商品每天获得的利润为![]() 元,则每天的销售量应为多少件?
元,则每天的销售量应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
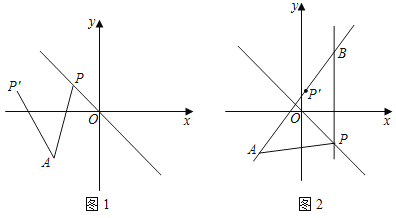
【题目】如图1,点P(m,n)在一次函数y=﹣x的图象上,将点P绕点A(﹣![]() ,﹣
,﹣![]() )逆时针旋转45°,旋转后的对应点为P′.
)逆时针旋转45°,旋转后的对应点为P′.
(1)当m=0时,求点P′的坐标;
(2)试说明:不论m为何值,点P′的纵坐标始终不变;
(3)如图2,过点P作x轴的垂线交直线AP′于点B,若直线PB与二次函数y=﹣x2﹣x+2的图象交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com