
【题目】过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.
(1)如图,在等腰![]() 中,
中,![]() ,
,![]() .
.
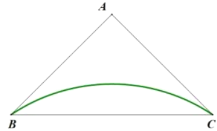
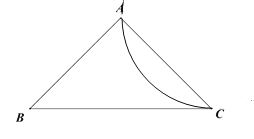
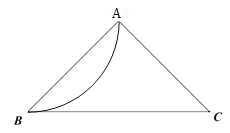
①在下图中画出一条![]() 的形内弧;
的形内弧;
②在![]() 中,其形内弧的长度最长为______.
中,其形内弧的长度最长为______.
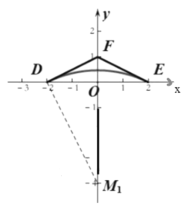
(2)在平面直角坐标系中,点![]() ,
,![]() ,
,![]() .点M为
.点M为![]() 形内弧所在圆的圆心.求点M纵坐标
形内弧所在圆的圆心.求点M纵坐标![]() 的取值范围;
的取值范围;
(3)在平面直角坐标系中,点![]() ,点G为x轴上一点.点P为
,点G为x轴上一点.点P为![]() 最长形内弧所在圆的圆心,求点P纵坐标
最长形内弧所在圆的圆心,求点P纵坐标![]() 的取值范围.
的取值范围.
【答案】(1)①见解析;②当![]() 时,
时,![]() 的形内弧最长,此时弧长
的形内弧最长,此时弧长![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1) ①根据形内弧的定义作图即可得到答案;②根据题意得到当![]() 时,
时,![]() 的形内弧最长,再根据弧长的计算公式即可得到答案;
的形内弧最长,再根据弧长的计算公式即可得到答案;
(2)分两种情况讨论,当圆心在x轴下方时,此时最长形内弧与线段![]() ,
,![]() 相切与当圆心在x轴上方时,此时最长形内弧与x轴相切分别求解即可得到答案;
相切与当圆心在x轴上方时,此时最长形内弧与x轴相切分别求解即可得到答案;
(3) 当![]() 时,最长形内弧与x轴相切,根据
时,最长形内弧与x轴相切,根据 ![]() 得到
得到![]() ,即
,即![]() ,再类似讨论另外几种情况,即可得到点P纵坐标
,再类似讨论另外几种情况,即可得到点P纵坐标![]() 的取值范围;
的取值范围;
解:(1)①如下图所作均可以:
②根据题意得到当![]() 时,
时,![]() 的形内弧最长,此时弧长
的形内弧最长,此时弧长![]() .
.
(2)当圆心在x轴下方时,此时最长形内弧与线段![]() ,
,![]()
![]() ,
,
∴![]() (相似三角形对应边成比例),
(相似三角形对应边成比例),
![]()
![]()
![]()
当圆心在x轴上方时,此时最长形内弧与x轴相切
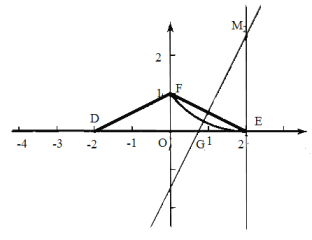
![]() ,
,
∴![]() ,
,
∵![]() ,FO=1,FE=
,FO=1,FE=![]() ,
,
![]()
![]()
综上所述,![]() 或
或![]()
(3)当![]() 时,最长形内弧与x轴相切
时,最长形内弧与x轴相切
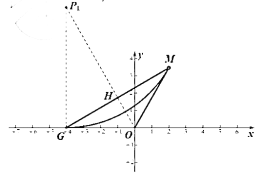
若xG=-4时,
![]() ,
,
![]() ,
,
![]() ;
;
当![]() 时,此时最长形内弧与线段
时,此时最长形内弧与线段![]() 相切,
相切,
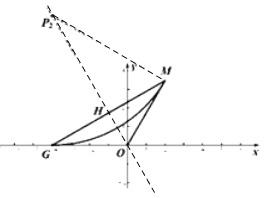
解得![]() ;
;
当![]() 时,此时最长形内弧与线段
时,此时最长形内弧与线段![]() 相切,
相切,

解得![]() ;
;
当![]() 时,此时最长形内弧与线段
时,此时最长形内弧与线段![]() 相切,
相切,
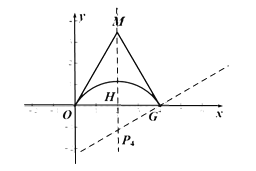
解得![]() ,
,
综上所述,![]() 或
或![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
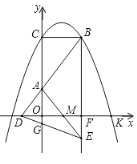
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(-1,0),交y轴于点C.
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴,y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;
(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
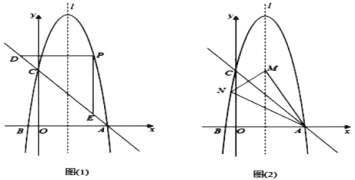
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,P是
,P是![]() 上的动点,D是
上的动点,D是![]() 延长线上的定点,连接
延长线上的定点,连接![]() 交
交![]() 于点Q.
于点Q.
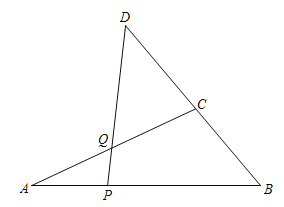
小明根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在![]() 上的不同位置,画图测量,得到了线段
上的不同位置,画图测量,得到了线段![]() 的长度(单位:cm)的几组值,如下表:
的长度(单位:cm)的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
| 4.99 | 4.56 | 4.33 | 4.23 | 4.53 | 4.95 | 5.51 |
| 4.99 | 3.95 | 3.31 | 2.95 | 2.80 | 2.79 | 2.86 |
在![]() 的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度约为_______cm.
的长度约为_______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]()
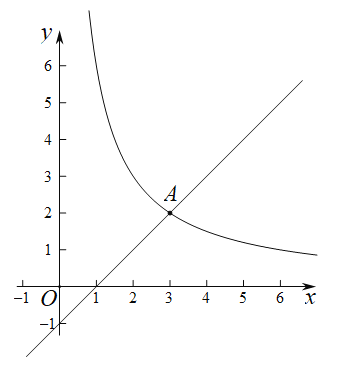
(1)求k的值;
(2)已知点![]() ,过点P作垂直于x轴的直线,交直线
,过点P作垂直于x轴的直线,交直线![]() 于点B,交函数
于点B,交函数![]() 于点C.
于点C.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合图象,直接写出n的取值范围.
,结合图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月至5月,某校开展了一系列居家阅读活动.学生利用“宅家”时光,在书海中遨游,从阅读中获得精神慰藉和自我提升.为了解学生居家阅读的情况,学校从七、八两个年级各随机抽取50名学生,进行了居家阅读情况调查.下面给出了部分数据信息:
![]() .两个年级学生平均每周阅读时长
.两个年级学生平均每周阅读时长![]() (单位:小时)的频数分布直方图如下(数据分成4组:
(单位:小时)的频数分布直方图如下(数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):

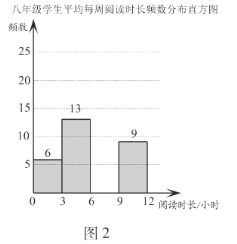
b.七年级学生平均每周阅读时长在![]() 这一组的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
这一组的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
c.两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
七年级 | 6.3 |
| 8 | 7.0 |
八年级 | 6.0 | 7 | 7 | 6.3 |
根据以上信息,回答下列问题:
(1)补全图2;
(2)写出表中![]() 的值;
的值;
(3)返校后,学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号.小丽说:“根据频数分布直方图中的数据信息,估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,所以七年级获得该称号的人数一定比八年级获得该称号的人数多.”你认为她的说法________(填入“正确”或“错误”);
(4)请你结合数据对两个年级的居家阅读情况进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )
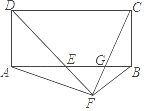
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片 ABCD中,AB=3,点P,Q分别是AB和CD的中点,现将这张纸片折叠,使点D落到PQ上的点G处,折痕为CH,若HG的延长线恰好经过点B,则AD的长为_____.
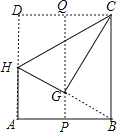
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com