
【题目】2020年3月至5月,某校开展了一系列居家阅读活动.学生利用“宅家”时光,在书海中遨游,从阅读中获得精神慰藉和自我提升.为了解学生居家阅读的情况,学校从七、八两个年级各随机抽取50名学生,进行了居家阅读情况调查.下面给出了部分数据信息:
![]() .两个年级学生平均每周阅读时长
.两个年级学生平均每周阅读时长![]() (单位:小时)的频数分布直方图如下(数据分成4组:
(单位:小时)的频数分布直方图如下(数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):

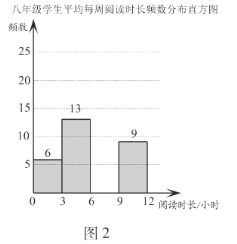
b.七年级学生平均每周阅读时长在![]() 这一组的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
这一组的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
c.两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
七年级 | 6.3 |
| 8 | 7.0 |
八年级 | 6.0 | 7 | 7 | 6.3 |
根据以上信息,回答下列问题:
(1)补全图2;
(2)写出表中![]() 的值;
的值;
(3)返校后,学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号.小丽说:“根据频数分布直方图中的数据信息,估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,所以七年级获得该称号的人数一定比八年级获得该称号的人数多.”你认为她的说法________(填入“正确”或“错误”);
(4)请你结合数据对两个年级的居家阅读情况进行评价.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天,求甲、乙两厂每天能生产口罩多少万只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.
(1)该商场购进这种彩灯的实际进价为多少元?
(2)该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是5G爆发元年,三大运营商都在政策的支持下,加快着5G建设的步伐.某通信公司实行的5G畅想套餐,部分套餐资费标准如下:
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
套餐2 | 158 | 40 | 300 | ||
套餐3 | 198 | 60 | 500 | ||
套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.
(1)如图,在等腰![]() 中,
中,![]() ,
,![]() .
.
①在下图中画出一条![]() 的形内弧;
的形内弧;
②在![]() 中,其形内弧的长度最长为______.
中,其形内弧的长度最长为______.
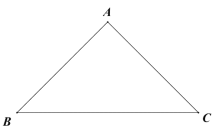
(2)在平面直角坐标系中,点![]() ,
,![]() ,
,![]() .点M为
.点M为![]() 形内弧所在圆的圆心.求点M纵坐标
形内弧所在圆的圆心.求点M纵坐标![]() 的取值范围;
的取值范围;
(3)在平面直角坐标系中,点![]() ,点G为x轴上一点.点P为
,点G为x轴上一点.点P为![]() 最长形内弧所在圆的圆心,求点P纵坐标
最长形内弧所在圆的圆心,求点P纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,则∠CMA的度数为( )
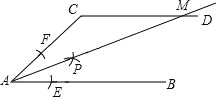
A.30°B.35°C.70°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,做BD的垂直平分线E,F,分别与AD、BC交于点E、F,连接BE,DF,若EF=AE+FC,则边BC的长为( )
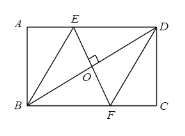
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,以二次函数![]() 的二次项系数
的二次项系数![]() 的2倍为一次项系数,一次项系数
的2倍为一次项系数,一次项系数![]() 为常数项构造的一次函数
为常数项构造的一次函数![]() 叫做二次函数
叫做二次函数![]() 的“子函数”,反过来,二次函数
的“子函数”,反过来,二次函数![]() 叫做一次函数
叫做一次函数![]() 的“母函数”.
的“母函数”.
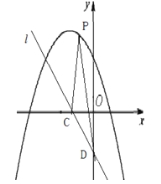
(1)若一次函数![]() 是二次函数
是二次函数![]() 的“子函数”,且二次函数经过点
的“子函数”,且二次函数经过点![]() ,求此二次函数的解析式.
,求此二次函数的解析式.
(2)如图,已知二次函数![]() 的“子函数”图象直线
的“子函数”图象直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 是直线
是直线![]() 上方的抛物线上任意一点,求
上方的抛物线上任意一点,求![]() 的面积的最大值.
的面积的最大值.
(3)已知二次函数![]() 与它的“子函数”
与它的“子函数”![]() 的函数图象有两个交点
的函数图象有两个交点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
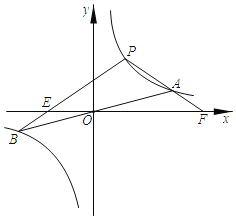
【题目】如图,双曲线y1=![]() 与直线y2=
与直线y2=![]() 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=![]() 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.
(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=![]() 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com