
分别以▱ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.
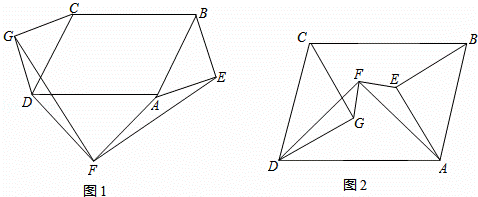
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,
∠EAF=360°﹣∠BAE﹣∠DAF﹣∠BAD=270°﹣(180°﹣∠CDA)=90°+∠CDA,
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
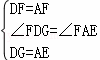 ,
,
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF,GF=EF;
(2)GF⊥EF,GF=EF成立;
理由:∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠BAE+∠DAF+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°,
∵∠CDF+∠GDF=45°,
∴∠FDG=∠EAF,
∵在△GDF和△EAF中,
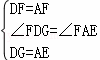 ,
,
∴△GDF≌△EAF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF,GF=EF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,直线y=mx与双曲线y=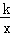 相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)根据图象直接写出当mx>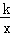 时,x的取值范围.
时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数最多是( )

A. 7个 B. 8个 C. 9个 D. 10个
查看答案和解析>>
科目:初中数学 来源: 题型:
实数tan45°,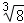 ,0,﹣
,0,﹣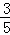 π,
π,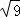 ,﹣
,﹣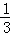 ,sin60°,0.3131131113…(相邻两个3之间依次多一个1),其中无理数的个数是( )
,sin60°,0.3131131113…(相邻两个3之间依次多一个1),其中无理数的个数是( )
A. 4 B. 2 C. 1 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为( )
A. 8 B. 20 C. 8或20 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为 上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.
上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.
(1)求证:QN=QF;
(2)若点E到弦MH的距离为1,cos∠Q= ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com