
如图(1),边长为6的等边三角形ABC中,点D沿射线AB方向由A向B运动,点F同时从C出发,以相同的速度沿射线BC方向运动,过点D作DE⊥AC,连结DF交射线AC于点G.

(1)当点D运动到AB的中点时,求AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图(2)的情况时,EG的长始终等于AC的一半吗?若改变,说明理由,若不变,请证明EG等于AC的一半.
(1) ;(2)2,
;(2)2, ,(3)不变,证明见试题解析.
,(3)不变,证明见试题解析.
【解析】
试题分析:(1)解直角三角形ADE,根据30°角对应直角边为斜边长一半即可解题;
(2)设AD=X,解直角三角形BDF即可求得X的值,即可求得△BDF的面积;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
试题解析:(1)当D为AB中点时,AD=3,
在RT△ADE中,∠A=60°,∠ADE=30°,∴AE=AD•sinA= .
.
(2)设AD=x,则CF=x,
当DF⊥AB时,RT△BDF中,∠F=30°,∴BF=2BD,6+x=2(6﹣x),解得x=2,∴AD=2.
∴BD=6﹣2=4,
DF=BD•tanB= ,∴△BDF的面积为
,∴△BDF的面积为 BD•DF=
BD•DF= .
.
(3)过F作FH⊥AC,

在△ADE和△CFH中,∵∠AED=∠FHC,∠A=∠FCH,AD=CF,∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,∴AC=EH,
在△GDE和△GFH中,∵∠DEG=∠FHG,∠DGE=∠FGH,DE=FH,∴△GDE≌△GFH(AAS),
∴EG=GH,∴EG= EH=
EH= AC.
AC.
考点:1.全等三角形的判定与性质;2.等边三角形的判定与性质.


科目:初中数学 来源:2014-2015学年浙江省富阳市共同体九年级10月月考数学试卷(解析版) 题型:填空题
将抛物线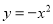 先向右平移1个单位,再向上平移5个单位,得到的抛物线的解析式是 .
先向右平移1个单位,再向上平移5个单位,得到的抛物线的解析式是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省联盟八年级上学期期中数学试卷(解析版) 题型:选择题
如图,∠1=750,AB=BC=CD=DE=EF,则∠A 的度数为( )
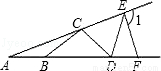
A.150 B.200 C.250 D.300
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州地区九年级上学期期中质量检测数学试卷(解析版) 题型:选择题
二次函数 的图象上有两点(3,a)和(-5,a),则此拋物线的对称轴是( )
的图象上有两点(3,a)和(-5,a),则此拋物线的对称轴是( )
A.直线 B.直线
B.直线 C.直线
C.直线 D.直线
D.直线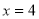
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州地区九年级上学期期中质量检测数学试卷(解析版) 题型:选择题
某小区现有一块等腰直角三角形形状的绿地,腰长为100米,直角顶点为A.小区物业管委会准备把它分割成面积相等的两块,有如下的分割方法:方法一:在底边BC上找一点D,连接AD作为分割线;
方法二:在腰AC上找一点D,连接BD作为分割线;
方法三:在腰AB上找一点D,作DE∥BC,交AC于点E,DE作为分割线;
方法四:以顶点A为圆心,AD为半径作弧,交AB于点D,交AC于点E,弧DE作为分割线.

这些分割方法中分割线最短的是( )
A.方法一 B.方法二 C.方法三 D.方法四
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州地区九年级上学期期中质量检测数学试卷(解析版) 题型:解答题
(本小题满分10分)在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率;
(2)从中任取一球,将球上的数字记为a,求关于x的一元二次方程 有实数根的概率;
有实数根的概率;
(3)从中任取一球,将球上的数字作为点的横坐标记为x(不放回);在任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市联盟学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.

(1)求∠ACB的大小;
(2)写出A,B两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com