
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD,∠ADC的平分线DE,交BC于点E.
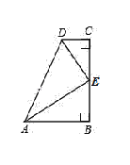
证明:①EC=EB;②AE⊥DE.
【答案】见解析
【解析】
(1)过点E作EF⊥AD于F,根据角平分线上的点到角的两边距离相等可得CE=EF,再求出BE=EF,从而得出结论.
(2)证AE是∠DAB的角平分线,即可求出答案.
证明:(1)如图,过点E作EF⊥AD于F,
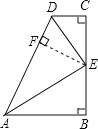
∵∠B=90°,DE平分∠CDA,
∴CE=EF,
又∵DE=DE,
∴RtDCE≌RtDFE.
∴DC=DF.
∵AD=AB+CD=DF+AF,
∴AB=AF.
又∵AE=AE,
∴RtAEB≌RtAFE.
∴EB=EF.
∴EB=CE.
(2)∵EB=CE,EF⊥AD,AB⊥BC,
∴AE平分∠BAD.
∵∠C=∠B=90°,
∴∠D+∠B=180°,
∴DC∥AB,
∴∠CDA+∠BAD=180°,
∵DE平分∠ADC,AE平分∠BAD,
∴∠EAD=![]() ∠BAD,∠EDA=
∠BAD,∠EDA=![]() ∠CDA,
∠CDA,
∴∠EAD+∠EDA=90°,
∴∠AED=180°﹣90°=90°.
∴AE⊥DE.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
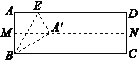

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
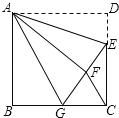
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)![]() ;
;
(9)![]() ;
;
(10)![]() ;
;
(11)20032;
(12)![]() ;
;
(13)![]() ;
;
(14)![]() ;
;
(15)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE是以C为公共顶点的两个等腰三角形,且AC=CB,CD=CE,连接BD、AE相交于点M,连接CM,∠CAB=∠CDE=50°,则∠BMC=( )

A. 30°B. 40°C. 50°D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com