
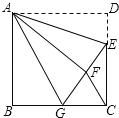
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
根据正方形性质和翻折的性质,得到AB=AF,∠B=∠AFG=90°,利用HL定理即可判定①正确;求出DE、CE的长,从而得到EF,设BG=x,然后表示出GF,再求出CG、EG的长,然后在Rt△CEG中,利用勾股定理列式求出x的值,从而得到BG=CG,判定②正确;再根据等边对等角的性质得到∠GCF=∠GFC,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠GCF+∠GFC=∠AGB+∠AGF,从而求出∠GCF=∠AGB,根据同位角相等,两直线平行即可证明AG∥CF,判定③正确;先求出△CEG的面积,再根据等高的三角形的面积的比等于底边的比求出△FGC的面积为![]() ,判定④错误.
,判定④错误.
解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=∠D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF,
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2,
∵CG=6-x,CE=4,EG=x+2
∴(6-x)2+42=(x+2)2
解得:x=3,
∴BG=GF=CG=3,
∴②正确;
∵CG=GF,
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG,
∴AG∥CF,
∴③正确;
∵△CFG和△CEG中,分别把FG和GE看作底边,
则这两个三角形的高相同.
∴![]() =
=![]() =
=![]() ,
,
∵S△CEG=![]() ×3×4=6,
×3×4=6,
∴S△FGC=![]() ×6=
×6=![]() ,
,
∴④错误;
正确的结论有3个.
故选C.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】某星期天早晨,小华从家出发步行前往体育馆锻炼,途中在报亭看了一会儿报,如图所示是小华从家到体育馆这一过程中所走的路程![]() 米
米![]() 与时间
与时间![]() 分
分![]() 之间的关系.
之间的关系.
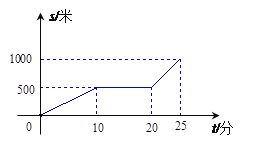
![]() 体育馆离小华家_______米,从出发到体育馆,小华共用了______分钟;
体育馆离小华家_______米,从出发到体育馆,小华共用了______分钟;
![]() 小华在报亭看报用了多少分钟?
小华在报亭看报用了多少分钟?
![]() 小华看完报后到体育馆的平均速度是多少?
小华看完报后到体育馆的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的最小值是( )

A. 5 B. 6 C. ![]() D.
D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,四边形ABCD是梯形,AB、CD相互平行,在AB上有两点E和F,此时四边形DCFE恰好是正方形,已知CD=a,AD=a+ab2,BC=a+2ab2,(单位:米)其中a>0,1<b2<4,现有甲乙两只妈蚁,甲蚂蚁从A点出发,沿着A﹣D﹣C﹣F﹣A的路线行走,乙蚂蚁从B点出发,沿着B﹣C﹣D﹣E﹣B的路线行走,甲乙同时出发,各自走回A和B点时停止.甲的速度是![]() (米/秒),乙的速度是
(米/秒),乙的速度是![]() (米/秒).
(米/秒).
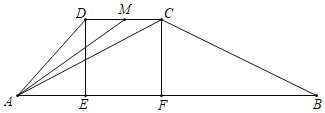
(1)用含a、b的代数式表示:
①甲走到点C时,用时 秒;
②当甲走到点C时,乙走了 米;
③当甲走到点C时,此时乙在点M处,△AMC的面积是 平方米;
④当甲走到点C时,已经和乙相遇一次,它们从出发到这一次相遇,用时 秒.
(2)它们还会有第二次相遇吗?如果有,请求出两只蚂蚁从出发到第二次相遇所用的时间.如果没有,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
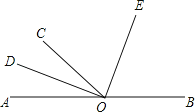
【题目】如图,点O为直线AB上一点,∠AOC=48°,OD平分∠AOC,OE⊥OD交于点O.
(1)求出∠BOD的度数;
(2)试用计算说明∠COE=∠BOE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD,∠ADC的平分线DE,交BC于点E.
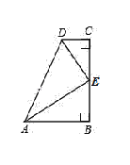
证明:①EC=EB;②AE⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英与她的父亲,母亲计划外出旅游,初步选择了延安、西安、汉中、安康四个城市,由于时间仓促,他们只能去其中一个城市,到底去哪一个城市三人意见不统一,在这种情况下,小英父亲建议,用小英学过的摸球游戏来决定,规则如下:
①在一个不透明的袋子中装一个红球(延安)、一个白球(西安)、一个黄球(汉中)和一个黑球(安康),这四个球除颜色的不同外,其余完全相同;
②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀;然后让小英母亲从袋中随机摸出一球,父亲记录下它的颜色;
③若两人所摸出球的颜色相同,则去该球所表示的城市旅游。否则,前面的记录作废,按规则②重新摸球,直到两人所摸出的球的颜色相同为止。
按照上面的规则,请你解答下列问题:
(1)已知小英的理想旅游城市是西安,小英和母亲随机各摸球一次,均摸出白球的概率是多少?
(2)已知小英母亲的理想旅游城市是汉中,小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com