
����Ŀ����֪����ͼ���ı���ABCD�����Σ�AB��CD�ƽ�У���AB��������E��F����ʱ�ı���DCFEǡ���������Σ���֪CD��a��AD��a+ab2��BC��a+2ab2������λ���ף�����a��0��1��b2��4�����м�����ֻ���ϣ������ϴ�A�����������A��D��C��F��A��·�����ߣ������ϴ�B�����������B��C��D��E��B��·�����ߣ�����ͬʱ������������A��B��ʱֹͣ�����ٶ���![]() ����/�룩���ҵ��ٶ���
����/�룩���ҵ��ٶ���![]() ����/�룩��
����/�룩��
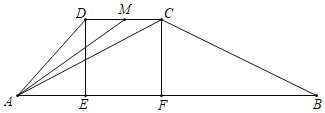
��1���ú�a��b�Ĵ���ʽ��ʾ��
�����ߵ���Cʱ����ʱ�� ���룻
�������ߵ���Cʱ�������������ף�
�������ߵ���Cʱ����ʱ���ڵ�M������AMC�����������ƽ���ף�
�������ߵ���Cʱ���Ѿ���������һ�Σ����Ǵӳ�������һ����������ʱ�����룮
��2�����ǻ����еڶ�������������У��������ֻ���ϴӳ������ڶ����������õ�ʱ�䣮���û�У���Ҫ˵�����ɣ�
���𰸡���1������12+6b2��������3a+![]() ��������a2��
��������a2��![]() a2b2������
a2b2������![]() ����2����ֻ���ϴӳ������ڶ����������õ�ʱ����
����2����ֻ���ϴӳ������ڶ����������õ�ʱ����![]() �룮
�룮
��������
��1���ٸ���·�����ٶ�=ʱ��ɵý��ۣ�
�ڸ����ٶ���ʱ��=·�̿ɵý��ۣ�
�۸��������ε������ʽ�ɵý��ۣ�
����һ����������ʱt�룬������·�̺�=AD+CD+BC�з��̿ɵý��ۣ�
��2��������·��=AD+CD+CF+EF+DE+CD+BC���з��̿ɵý��ۣ�
��1�������ߵ���Cʱ����ʱ�� ����12+6b2���룻
����12+6b2���룻
�ʴ�Ϊ����12+6b2����
��![]() a��12+6b2����3a+
a��12+6b2����3a+![]()
���ߵ���Cʱ�������ˣ�3a+![]() ���ף�
���ף�
�ʴ�Ϊ����3a+![]() ����
����
��CM��BM��BC����3a+![]() ������a+2ab2����2a��
������a+2ab2����2a��![]() ab2��
ab2��
���AMC�������![]() ��
��![]() ��a2��
��a2��![]() a2b2��
a2b2��
���ߵ���Cʱ����ʱ���ڵ�M������AMC������ǣ�a2��![]() a2b2��ƽ���ף�
a2b2��ƽ���ף�
�ʴ�Ϊ����a2��![]() a2b2����
a2b2����
������һ����������ʱt�룬
��������ã�![]() at+
at+![]() at��a+ab2+a+a+2ab2��
at��a+ab2+a+a+2ab2��
t��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2�����軹�еڶ�����������ڶ���x��ʱ���������ʱһ��������EF�ϣ�
��������ã�![]() at+
at+![]() at��a+ab2+3a+2a+a+2ab2��
at��a+ab2+3a+2a+a+2ab2��
x��![]() ��
��
����ֻ���ϴӳ������ڶ����������õ�ʱ����![]() �룮
�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(8��) С������һ�����Ϊ400cm2��������ֽƬ,���űߵķ���ô�һ�����Ϊ300cm2�ij�����ֽƬ.(1)���С�����һ�ֿ��еIJü�����;
(2)��ʹ�����εij���֮��Ϊ3:2,С���������ֽƬ�ô�����Ҫ���ֽƬ������,���С�����һ�ֲü�����,�����ܣ����Ҫ˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��
��![]() ������A��ʾ����Ϊ-2��
������A��ʾ����Ϊ-2��![]() ��ʾ����Ϊ2�����������ϴ���һ��
��ʾ����Ϊ2�����������ϴ���һ��![]() ��ʹ��
��ʹ��![]() ����Ƶ�
����Ƶ�![]() ������
������![]() ��
��![]() ����
����![]() �ڵ���������ͼ1��ʾ������
�ڵ���������ͼ1��ʾ������![]() ��ʾ����Ϊ0����
��ʾ����Ϊ0����![]() ����Ƶ�
����Ƶ�![]() Ϊ��
��![]() ��
��![]() ����4�ڵ���.
����4�ڵ���.
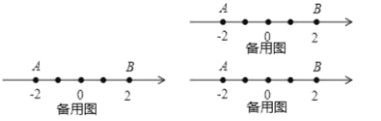
����������涨�ش��������⣺
��1������![]() ��
��![]() ��
��![]() ����
����![]() �ڵ������ҵ�
�ڵ������ҵ�![]() �������ϱ�ʾ����Ϊ-4����
�������ϱ�ʾ����Ϊ-4����![]() ��ֵ.
��ֵ.
��2������![]() �������ϵ�
�������ϵ�![]() ��
��![]() ����5�ڵ���������ֱ��д����
����5�ڵ���������ֱ��д����![]() ��ʾ����Ϊ____________��
��ʾ����Ϊ____________��
��3������![]() �������ϣ�����
�������ϣ�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ֮��ľ�����
֮��ľ�����![]() ��
��![]() ֮������һ�룬�Ҵ�ʱ��
֮������һ�룬�Ҵ�ʱ��![]() Ϊ��
��![]() ��
��![]() ����
����![]() �ڵ�������
�ڵ�������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽƬABCD�����۵�������������£�
��һ�����ȶ��ۣ�ʹAD��BC�غϣ��õ��ۺ�MN��չ����
�ڶ�������һ���۵���ʹ��A����MN�ϵĵ�A��������ʹ�ۺ۾�����B���õ��ۺ�BE��ͬʱ���õ��߶�BA�䣬EA����չ������ͼ1��
������������EA�����ڵ�ֱ���۵�����B����AD�ϵĵ�B�������õ��ۺ�EF��ͬʱ�õ��߶�B��F��չ������ͼ2.
��֤��(1)��ABE��30�㣻
(2)�ı���BFB��EΪ���Σ�
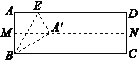

ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ6cm��������ABCD�۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G������EBG���ܳ��� cm��
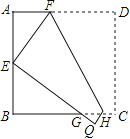
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��6����E�ڱ�CD�ϣ���CD��3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ�����ABG�ա�AFG����BG��GC����AG��CF����S��FGC��3��������ȷ���۵ĸ����ǣ�������
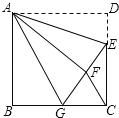
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��BC��DC��EC��AC=BC��DC=EC��ͼ��AE��BD�������Ĺ�ϵ��������ϵ��λ�ù�ϵ������֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У��뾶OA��OB����OA���е�C��FD��OB����O��D��F���㣬��CD��![]() ����OΪԲ�ģ�OCΪ�뾶��
����OΪԲ�ģ�OCΪ�뾶��![]() ����OB��E�㣮
����OB��E�㣮
��1�����O�İ뾶OA�ij���
��2��������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ������˿�������ת����ת�̣���ͼ��ת�̱����ȷ�Ϊ20�ݣ������涨���˿�ÿ����200Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���200Ԫ��100Ԫ��50Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��תת�̣���ô����ֱ�ӻ�ù���ȯ30Ԫ��
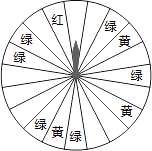
��1����ת��һ��ת�̻�ù���ȯ�ĸ��ʣ�
��2��תת�̺�ֱ�ӻ�ù���ȯ������Ϊ���ַ�ʽ�Թ˿����㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com