
【题目】已知数轴上两点![]() 、
、![]() ,其中A表示的数为-2,
,其中A表示的数为-2,![]() 表示的数为2,若在数轴上存在一点
表示的数为2,若在数轴上存在一点![]() ,使得
,使得![]() ,则称点
,则称点![]() 叫做点
叫做点![]() 、
、![]() 的“
的“![]() 节点”,例如图1所示,若点
节点”,例如图1所示,若点![]() 表示的数为0,有
表示的数为0,有![]() ,则称点
,则称点![]() 为点
为点![]() 、
、![]() 的“4节点”.
的“4节点”.
请根据上述规定回答下列问题:
(1)若点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,且点
节点”,且点![]() 在数轴上表示的数为-4,求
在数轴上表示的数为-4,求![]() 的值.
的值.
(2)若点![]() 是数轴上点
是数轴上点![]() 、
、![]() 的“5节点”,请你直接写出点
的“5节点”,请你直接写出点![]() 表示的数为____________;
表示的数为____________;
(3)若点![]() 在数轴上(不与
在数轴上(不与![]() 、
、![]() 重合),满足
重合),满足![]() 、
、![]() 之间的距离是
之间的距离是![]() 、
、![]() 之间距离的一半,且此时点
之间距离的一半,且此时点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,求
节点”,求![]() 的值.
的值.
【答案】(1)8;(2)![]() ;(3)4或12
;(3)4或12
【解析】
(1)利用"n节点"的概念进行解答即可;
(2)设点D表示的数为x,由"5节点"的定义列出方程分情况进行解答;
(3)根据点E的不同位置:①当点E在BA延长线上时;②当点E在线段AB上时;③当点E在AB延长线上时,根据BE=![]() AE,先求点E表示的数,再根据AC+BC=n,列方程解答即可.
AE,先求点E表示的数,再根据AC+BC=n,列方程解答即可.
解:(1)由A表示的数为-2,B表示的数为2,点C在数轴上表示的数为-4,
∴AC=2,BC=6,
∴n=AC+BC-2+6=8.
(2)如图:
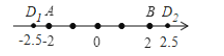
∵点D是数轴上点A、B的“5节点"
∴AC+BC=5,
∵AB=4
∴C在点A的左侧或在点A的右侧,
设点D表示的数为x,则AC+BC=5,
∴-2-x+2-x=5或x-2+x-(-2)=5,x=-2.5或2.5,
则点D表示的数为2.5或-2.5;
(3) 根据点E和BE的位置关系,需分三种情况:
①当点E在BA延长线上时,BE不可能等于![]() AE,故舍弃;
AE,故舍弃;
②当点E在线段AB上时,满足BE=![]() AE,如图:
AE,如图:
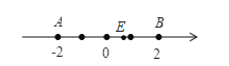
∴n=AE+BE=AB=4;
③当点E在AB延长线上时,如图:
![]()
∵BE=![]() AE
AE
∴BE=AB=4,
∴点E表示的数为6,
则n=AE+BE=8+4=12
所以 n=4或n=12.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】随着各领域与“互联网+”有关产业的发展,滴滴专车、曹操专车等目前已经逐步占据各城市的营运行业的主要营业份额.为了更好的吸引客户群,提高服务品质,“曹操专车”和“滴滴专车”通过不同的收费方式吸引顾客,“曹操专车”的收费标准为3公里以内(含3公里)起步价15元,超过3公里后每公里加收1.8元;“滴滴专车”收费标准为3公里以内(含3公里)起步价10元,超过3公里后每公里加收2.5元.
(1)若顾客乘坐专车2公里,选择 (填“曹操”或“滴滴”)专车更为合算.
(2)若顾客乘坐专车![]() 公里(
公里(![]() ,且
,且![]() 为正整数),请用含
为正整数),请用含![]() 的代数式分别表示乘坐滴滴专车和曹操专车的收费情况.
的代数式分别表示乘坐滴滴专车和曹操专车的收费情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
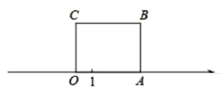
【题目】如图1,长方形![]() 的边
的边![]() 在数轴上,
在数轴上,![]() 为原点,长方形
为原点,长方形![]() 的面积为12,
的面积为12,![]() 边的长为3
边的长为3
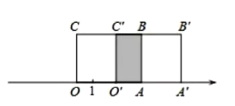
(1)数轴上点![]() 表示的数为
表示的数为
(2)将长方形![]() 沿数轴水平移动,移动后的长方形记为
沿数轴水平移动,移动后的长方形记为![]() ,设长方形
,设长方形![]() 移动的距离为
移动的距离为![]() ,移动后的长方形
,移动后的长方形![]() 与原长方形
与原长方形![]() 重叠部分的面积记为
重叠部分的面积记为![]()
①当![]() 等于原长方形
等于原长方形![]() 面积的
面积的![]() 时,则点
时,则点![]() 的移动距离
的移动距离![]() ,此时数轴上点
,此时数轴上点![]() 表示的数为
表示的数为
②![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() 当点
当点![]() 所表示的数互为相反数时,则
所表示的数互为相反数时,则![]() 的值为
的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE与AD相交于点F,∠EDF=38°,则∠DBE的度数是( )
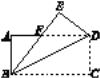
A. 25° B. 26° C. 27° D. 38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,E是AB的中点,F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的最小值是( )

A. 5 B. 6 C. ![]() D.
D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC 中,∠BAC=90°,AB=AC,过 A 任作一直线 l,作 BD⊥l于 D,CE⊥l于 E,观察三条线段 BD,CE,DE 之间的数量关系.
(1)如图 1,当 l 经过 BC 中点时,此时 BD CE;
(2)如图 2,当 l 不与线段 BC 相交时,BD,CE,DE 三者的数量关系为 ,并证明 你的结论.
(3 )如图 3 ,当 l 与线段 BC 相交,交点靠近 B 点时,BD ,CE ,DE 三者的数量关系 为 .证明你的结论,并画图直接写出交点靠近 C 点时,BD,CE,DE 三者的数最关 系为 .
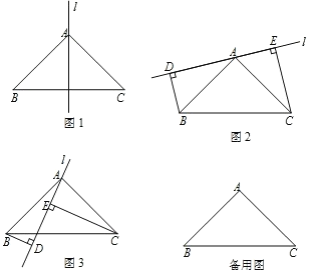
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,四边形ABCD是梯形,AB、CD相互平行,在AB上有两点E和F,此时四边形DCFE恰好是正方形,已知CD=a,AD=a+ab2,BC=a+2ab2,(单位:米)其中a>0,1<b2<4,现有甲乙两只妈蚁,甲蚂蚁从A点出发,沿着A﹣D﹣C﹣F﹣A的路线行走,乙蚂蚁从B点出发,沿着B﹣C﹣D﹣E﹣B的路线行走,甲乙同时出发,各自走回A和B点时停止.甲的速度是![]() (米/秒),乙的速度是
(米/秒),乙的速度是![]() (米/秒).
(米/秒).
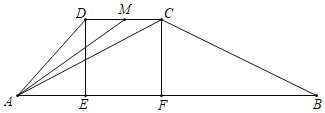
(1)用含a、b的代数式表示:
①甲走到点C时,用时 秒;
②当甲走到点C时,乙走了 米;
③当甲走到点C时,此时乙在点M处,△AMC的面积是 平方米;
④当甲走到点C时,已经和乙相遇一次,它们从出发到这一次相遇,用时 秒.
(2)它们还会有第二次相遇吗?如果有,请求出两只蚂蚁从出发到第二次相遇所用的时间.如果没有,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行单项式:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;①
,…;①
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;②
,…;②
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,…;③
,…;③
根据你发现的规律,解答下列问题:
(1)第①行的第8个单项式为 ;
(2)第②行的第9个单项式为 ;
(3)第③行的第n个单项式为 (用含n的式子表示);
(4)取每行的第8个单项式,令这三个单项式的和为A.
当![]() 时,求A的值.
时,求A的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com