【题目】如图，△ABC和△CDE是以C为公共顶点的两个等腰三角形，且AC=CB，CD=CE，连接BD、AE相交于点M，连接CM，∠CAB=∠CDE=50°，则∠BMC=（ ）
A. 30°B. 40°C. 50°D. 60°
培优三好生系列答案
优化作业上海科技文献出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，在矩形纸片ABCD中，AB＝2，AD＝3，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的最小值是( )
A. 5 B. 6 C. 
D. －1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，∠B＝∠C＝90°，AB＞CD，AD＝AB+CD,∠ADC的平分线DE，交BC于点E.
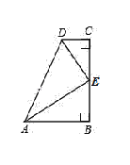
证明：①EC＝EB；②AE⊥DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面三行单项式：
， 
，
，
，
，
，…；①
，，
，，
，，…；②
，
，
，
， 
，
，…；③
根据你发现的规律，解答下列问题：
（1）第①行的第8个单项式为 ；
（2）第②行的第9个单项式为 ；
（3）第③行的第n个单项式为 (用含n的式子表示)；
（4）取每行的第8个单项式，令这三个单项式的和为A.
当
时，求A的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
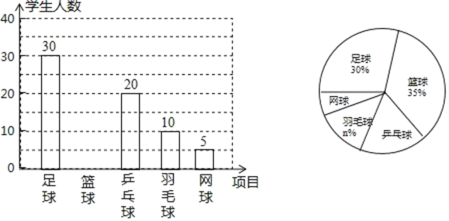
【题目】深圳高级中学(集团)开展“阳光体育活动”，共开设足球，蓝球，乒乓球，羽毛球，网球五项活动，为了了解学生对这五项活动的喜爱情况，随机调查了m名学生(每名学生必须且只能选择这五项运动中的一种)，并根据调查的结果绘制了如图所示不完整的统计图．根据以上统计图提供的信息，解答下列问题：
（1）m= ，n= ；
（2）补全条形统计图；
（3）若深高(集团)共有学生6000人，则喜欢乒乓球的约有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是正方形，E是线段CD上的点，将△ADE沿AE对折得到△AFE，直线EF交边BC于点G，连接AG.
(1)求证：△ABG≌△AFG；
(2)当DE是CD的一半时，求∠EAG的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小英与她的父亲，母亲计划外出旅游，初步选择了延安、西安、汉中、安康四个城市，由于时间仓促，他们只能去其中一个城市，到底去哪一个城市三人意见不统一，在这种情况下，小英父亲建议，用小英学过的摸球游戏来决定，规则如下：
①在一个不透明的袋子中装一个红球（延安）、一个白球（西安）、一个黄球（汉中）和一个黑球（安康），这四个球除颜色的不同外，其余完全相同；
②小英父亲先将袋中球摇匀，让小英从袋中随机摸出一球，父亲记录下其颜色，并将这个球放回袋中摇匀；然后让小英母亲从袋中随机摸出一球，父亲记录下它的颜色；
③若两人所摸出球的颜色相同，则去该球所表示的城市旅游。否则，前面的记录作废，按规则②重新摸球，直到两人所摸出的球的颜色相同为止。
按照上面的规则，请你解答下列问题：
（1）已知小英的理想旅游城市是西安，小英和母亲随机各摸球一次，均摸出白球的概率是多少？
（2）已知小英母亲的理想旅游城市是汉中，小英和母亲随机各摸球一次，至少有一人摸出黄球的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）求证：OE=OF；
（2）若CE=12，CF=5，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
