
【题目】如图,四边形ABCD是正方形,E是线段CD上的点,将△ADE沿AE对折得到△AFE,直线EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)当DE是CD的一半时,求∠EAG的度数.

【答案】(1)证明见解析(2)45°
【解析】
(1)由正方形的性质和折叠的性质易得AB=AD=AF,∠B=∠D=∠AFE=∠AFG=90°,这样结合AG=AG即可由“HL”证得△ABG≌△AFG;
(2)由折叠的性质可得∠EAF=∠EAD,由(1)中所当△ABG≌△AFG可得∠FAG=∠BAG,这样结合在正方形ABCD中,∠BAD=90°即可得到∠EAG=∠EAF+∠GAF=![]() ∠BAD=45°.
∠BAD=45°.
(1)∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°.
∵将△ADE沿AE对折得到△AFE,
∴AF=AD=AB,∠AFE=∠D=90°.
在Rt△ABG和Rt△AFG中:![]() ,
,
∴Rt△ABG≌Rt△AFG(HL).
(2)∵由(1)可知:△ABG≌△AFG,
∴∠GAF=∠GAB.
∵△AFE是由△ADE沿AE折叠得到的,
∴∠EAF=∠EAD,
∵在正方形ABCD中,∠BAD=90°,
∴∠EAG=∠EAF+∠GAF=![]() ×90°=45°.
×90°=45°.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
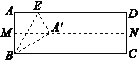

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE是以C为公共顶点的两个等腰三角形,且AC=CB,CD=CE,连接BD、AE相交于点M,连接CM,∠CAB=∠CDE=50°,则∠BMC=( )

A. 30°B. 40°C. 50°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
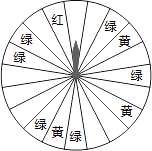
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为

A. 36° B. 40° C. 45° D. 50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com