
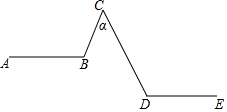
 如图,AB∥DE,∠α:∠D:∠B=2:3:4,求∠α.
如图,AB∥DE,∠α:∠D:∠B=2:3:4,求∠α.  一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
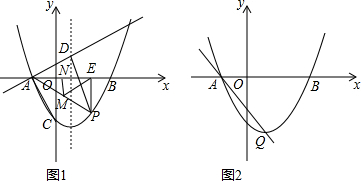
 如图,直线y=2x+1分别交于x、y轴于点A、C.P是该直线与双曲线y=$\frac{3}{x}$(x>0)的交点,PB⊥x轴,B为垂足,设点M与点P在同一个反比例函数的图象上,且点M在直线PB在右则,作MN⊥x轴,N为垂足,当△MNB与△AOC相似时,点M的坐标是($\frac{\sqrt{7}+1}{2}$,$\sqrt{7}$-1)或(3,1).
如图,直线y=2x+1分别交于x、y轴于点A、C.P是该直线与双曲线y=$\frac{3}{x}$(x>0)的交点,PB⊥x轴,B为垂足,设点M与点P在同一个反比例函数的图象上,且点M在直线PB在右则,作MN⊥x轴,N为垂足,当△MNB与△AOC相似时,点M的坐标是($\frac{\sqrt{7}+1}{2}$,$\sqrt{7}$-1)或(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
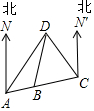 “奔跑吧,兄弟!”节目组,预设计一个新的游戏,“奔跑”需经A,B,C,D四点,如图,其中A,B,C三地在同一直线上,D点在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏,“奔跑”需经A,B,C,D四点,如图,其中A,B,C三地在同一直线上,D点在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com