Question

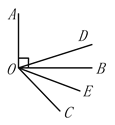
【题目】如图，DO平分∠AOC，OE平分∠BOC，若OA⊥OB，

（1）当∠BOC＝30°，∠DOE＝_______________； 当∠BOC＝60°，∠DOE＝_______________；

（2）通过上面的计算，猜想∠DOE的度数与∠AOB有什么关系，并说明理由．

Answer 1

【答案】 （1）45°， 45°；（2）∠DOE=∠AOB

【解析】试题分析：（1）先求出∠AOC，然后根据角平分线的定义求出∠COD和∠COE，最后根据∠DOE＝∠COD－∠COE进行计算即可；

（2）设∠AOB＝α，∠BOC＝β，仿照（1）中的求出进行计算即可．

试题解析：

（1）①∵OA⊥OB，∠BOC＝30°，

∴∠AOC＝90°＋30°＝120°，

∵OD平分∠AOC，OE平分∠BOC，

∴∠COD＝60°，∠COE＝15°，

∴∠DOE＝∠COD－∠COE＝60°－15°＝45°．

②∵OA⊥OB，∠BOC＝60°，

∴∠AOC＝90°＋60°＝150°，

∵OD平分∠AOC，OE平分∠BOC，

∴∠COD＝75°，∠COE＝30°，

∴∠DOE＝∠COD－∠COE＝75°－30°＝45°．

（2）∠DOE＝∠AOB．理由如下：

设∠AOB＝α，∠BOC＝β，

∵OD平分∠AOC，OE平分∠BOC，

∴∠COD＝（α＋β），∠COE＝β，

∴∠DOE＝∠COD－∠COE＝（α＋β－β）＝α＝∠AOB．