
ΓΨΧβΡΩΓΩΕ®“εΘΚΕ‘»Έ“β“ΜΗωΝΫΈΜ ΐ![]() Θ§»γΙϊ
Θ§»γΙϊ![]() ¬ζΉψΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷ΜΞ≤ΜœύΆ§Θ§«“ΕΦ≤ΜΈΣΝψΘ§Ρ«Ο¥≥Τ’βΗωΝΫΈΜ ΐΈΣΓΑεΡ“λ ΐΓ±Θ°ΫΪ“ΜΗωΓΑεΡ“λ ΐΓ±ΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷Ε‘ΒςΚσΒΟΒΫ“ΜΗω–¬ΒΡΝΫΈΜ ΐΘ§Α―’βΗω–¬ΝΫΈΜ ΐ”κ‘≠ΝΫΈΜ ΐΒΡΚΆ”κ
¬ζΉψΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷ΜΞ≤ΜœύΆ§Θ§«“ΕΦ≤ΜΈΣΝψΘ§Ρ«Ο¥≥Τ’βΗωΝΫΈΜ ΐΈΣΓΑεΡ“λ ΐΓ±Θ°ΫΪ“ΜΗωΓΑεΡ“λ ΐΓ±ΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷Ε‘ΒςΚσΒΟΒΫ“ΜΗω–¬ΒΡΝΫΈΜ ΐΘ§Α―’βΗω–¬ΝΫΈΜ ΐ”κ‘≠ΝΫΈΜ ΐΒΡΚΆ”κ![]() ΒΡ…ΧΦ«ΈΣ
ΒΡ…ΧΦ«ΈΣ![]() Θ°
Θ°
άΐ»γΘΚ![]() Θ§Ε‘ΒςΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷ΒΟΒΫ–¬ΝΫΈΜ ΐ
Θ§Ε‘ΒςΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷ΒΟΒΫ–¬ΝΫΈΜ ΐ![]() Θ§–¬ΝΫΈΜ ΐ”κ‘≠ΝΫΈΜ ΐΒΡΚΆΈΣ
Θ§–¬ΝΫΈΜ ΐ”κ‘≠ΝΫΈΜ ΐΒΡΚΆΈΣ![]() Θ§ΚΆ”κ
Θ§ΚΆ”κ![]() ΒΡ…ΧΈΣ
ΒΡ…ΧΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ°
Θ°
ΗυΨί“‘…œΕ®“εΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΧνΩ’ΘΚΔΌœ¬Ν–ΝΫΈΜ ΐΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷–Θ§ΓΑεΡ“λ ΐΓ±ΈΣ________Θ°
÷–Θ§ΓΑεΡ“λ ΐΓ±ΈΣ________Θ°
ΔΎΦΤΥψΘΚ![]() _________Θ§
_________Θ§![]() ________Θ°
________Θ°
Θ®2Θ©»γΙϊ“ΜΗωΓΑεΡ“λ ΐΓ±![]() ΒΡ °ΈΜ ΐΉ÷ «
ΒΡ °ΈΜ ΐΉ÷ «![]() Θ§ΗωΈΜ ΐΉ÷ «
Θ§ΗωΈΜ ΐΉ÷ «![]() Θ§«“
Θ§«“![]() ΘΜΝμ“ΜΗωΓΑεΡ“λ ΐΓ±
ΘΜΝμ“ΜΗωΓΑεΡ“λ ΐΓ±![]() ΒΡ °ΈΜ ΐΉ÷ «
ΒΡ °ΈΜ ΐΉ÷ «![]() Θ§ΗωΈΜ ΐΉ÷ «
Θ§ΗωΈΜ ΐΉ÷ «![]() Θ§«“
Θ§«“![]() Θ§«κ«σ≥ωΓΑεΡ“λ ΐΓ±
Θ§«κ«σ≥ωΓΑεΡ“λ ΐΓ±![]() ΚΆ
ΚΆ![]() Θ°
Θ°
Θ®3Θ©»γΙϊ“ΜΗωΓΑεΡ“λ ΐΓ±![]() ΒΡ °ΈΜ ΐΉ÷ «
ΒΡ °ΈΜ ΐΉ÷ «![]() Θ§ΗωΈΜ ΐΉ÷ «
Θ§ΗωΈΜ ΐΉ÷ «![]() Θ§Νμ“ΜΗωΓΑεΡ“λ ΐΓ±
Θ§Νμ“ΜΗωΓΑεΡ“λ ΐΓ±![]() ΒΡ °ΈΜ ΐΉ÷ «
ΒΡ °ΈΜ ΐΉ÷ «![]() Θ§ΗωΈΜ ΐΉ÷ «
Θ§ΗωΈΜ ΐΉ÷ «![]() Θ§«“¬ζΉψ
Θ§«“¬ζΉψ![]() Θ§«κ÷±Ϋ”–¥≥ω¬ζΉψΧθΦΰΒΡΥυ”–
Θ§«κ÷±Ϋ”–¥≥ω¬ζΉψΧθΦΰΒΡΥυ”–![]() ΒΡ÷Β________Θ°
ΒΡ÷Β________Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ21ΘΜΔΎ8ΘΜ![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©5Μρ7
ΘΜΘ®3Θ©5Μρ7
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌ”…ΓΑεΡ“λ ΐΓ±ΒΡΕ®“εΩ…ΒΟΘΜΔΎΗυΨίΕ®“εΦΤΥψΩ…ΒΟΘΜ
Θ®2Θ©”…![]() Θ§Ω…«σkΒΡ÷ΒΘ§Φ¥Ω…«σbΘΜ
Θ§Ω…«σkΒΡ÷ΒΘ§Φ¥Ω…«σbΘΜ
Θ®3Θ©ΗυΨίΧβ“βΩ…Ν–≥ω≤ΜΒ» ΫΘ§Ω…«σ≥ω5<x<9Θ§Φ¥Ω…«σxΒΡ÷Β.
Θ®1Θ©ΔΌΓΏΕ‘»Έ“β“ΜΗωΝΫΈΜ ΐaΘ§»γΙϊa¬ζΉψΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷ΜΞ≤ΜœύΆ§Θ§«“ΕΦ≤ΜΈΣΝψΘ§Ρ«Ο¥≥Τ’βΗωΝΫΈΜ ΐΈΣΓΑεΡ“λ ΐΓ±
ΓύΓΑεΡ“λ ΐΓ±ΈΣ21ΘΜ
ΔΎ![]() ΘΜ
ΘΜ
Θ®2Θ©ΓΏ![]() Θ§«“
Θ§«“![]()
Γύ![]()
Γύ![]()
Γύ![]() ΘΜ
ΘΜ
Θ®3Θ©ΓΏ![]()
Γύ![]() Θ§ΫβΒΟx<8
Θ§ΫβΒΟx<8
ΓΏx3>0Θ§x4>0
Γύx>4
Γύ4<x<8Θ§«“xΈΣ’ΐ’ϊ ΐ
Γύx=5Θ§6Θ§7
Β±x=5 ±Θ§m=52Θ§n=12Θ§
Β±x=6 ±Θ§m=63Θ§n=22(≤ΜΚœΧβ“βΘ§…α»Ξ)Θ§
Β±x=7 ±Θ§m=74Θ§n=32Θ§
Ήέ…œΥυ ωΘΚxΈΣ5Μρ7.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
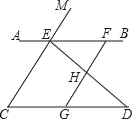
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψEΘ§F‘Ύ÷±œΏAB…œΘ§ΒψG‘ΎœΏΕΈCD…œΘ§ED”κFGΫΜ”ΎΒψHΘ§ΓœC=ΓœEFGΘ§ΓœCED=ΓœGHDΘ°
Θ®1Θ©«σ÷ΛΘΚCEΓΈGFΘΜ
Θ®2Θ© ‘≈–ΕœΓœAED”κΓœD÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τΓœEHF=70ΓψΘ§ΓœD=30ΓψΘ§«σΓœAEMΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ABCDΘ§Ε‘Ϋ«œΏACΘ§BDœύΫœ”ΎΒψOΘ§“Σ Ι
ABCDΘ§Ε‘Ϋ«œΏACΘ§BDœύΫœ”ΎΒψOΘ§“Σ Ι![]() ABCDΈΣΨΊ–ΈΘ§–ηΧμΦ”œ¬Ν–ΒΡ“ΜΗωΧθΦΰ «
ABCDΈΣΨΊ–ΈΘ§–ηΧμΦ”œ¬Ν–ΒΡ“ΜΗωΧθΦΰ «![]() ΓΓΓΓ
ΓΓΓΓ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΙΐAΒψΒΡ“Μ¥ΈΚ· ΐΒΡΆΦœσ”κ’ΐ±»άΐΚ· ΐyΘΫ2xΒΡΆΦœσœύΫΜ”ΎΒψB.
(1)«σ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
(2)≈–ΕœΒψC(4Θ§Θ≠2) «Ζώ‘ΎΗΟ“Μ¥ΈΚ· ΐΒΡΆΦœσ…œΘ§ΥΒΟςάμ”…ΘΜ
(3)»τΗΟ“Μ¥ΈΚ· ΐΒΡΆΦœσ”κx÷αΫΜ”ΎDΒψΘ§«σΓςBODΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ“Σ¥”ΆθΆ§―ßΚΆάνΆ§―ß÷–Χτ―Γ“Μ»Υ≤ΈΦ”œΊ÷Σ ΕΨΚ»ϋ‘ΎΈε¥Έ―ΓΑΈ≤β ‘÷–ΥϊΝ©ΒΡ≥…Φ®»γœ¬±μΘ°
ΒΎ1¥Έ | ΒΎ2¥Έ | ΒΎ3¥Έ | ΒΎ4¥Έ | ΒΎ5¥Έ | |
ΆθΆ§―ß | 60 | 75 | 100 | 90 | 75 |
άνΆ§―ß | 70 | 90 | 100 | 80 | 80 |
ΗυΨί…œ±μΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©Άξ≥…œ¬±μΘΚ
–’Οϊ | ΤΫΨυ≥…Φ®Θ®Ζ÷Θ© | ÷–ΈΜ ΐΘ®Ζ÷Θ© | ÷Ύ ΐΘ®Ζ÷Θ© | ΖΫ≤ν |
ΆθΆ§―ß | 80 | 75 | 75 | _____ |
άνΆ§―ß | ΓΓ ΓΓ | ΓΓ ΓΓ | ΓΓ ΓΓ | ΓΓ ΓΓ |
Θ®2Θ©‘Ύ’βΈε¥Έ≤β ‘÷–Θ§≥…Φ®±»ΫœΈ»Ε®ΒΡΆ§―ß «Υ≠»τΫΪ80Ζ÷“‘…œΘ®Κ§80Ζ÷Θ©ΒΡ≥…Φ® ”ΈΣ”≈–ψΘ§‘ρΆθΆ§―ßΓΔάνΆ§―ß‘Ύ’βΈε¥Έ≤β ‘÷–ΒΡ”≈–ψ¬ Ης «Εύ…ΌΘΩ
Θ®3Θ©άζΫλ±»»ϋ±μΟςΘ§≥…Φ®¥οΒΫ80Ζ÷“‘…œΘ®Κ§80Ζ÷Θ©ΨΆΚήΩ…ΡήΜώΫ±Θ§≥…Φ®¥οΒΫ90Ζ÷“‘…œΘ®Κ§90Ζ÷Θ©ΨΆΚήΩ…ΡήΜώΒΟ“ΜΒ»Ϋ±Θ§Ρ«Ο¥Ρψ»œΈΣ”Π―ΓΥ≠≤ΈΦ”±»»ϋ±»ΫœΚœ ΘΩΥΒΟςΡψΒΡάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΘΚ‘ΎΓςABCΘ§ΓςADE÷–Θ§ΓœBAC=ΓœDAE=90ΓψΘ§AB=ACΘ§AD=AEΘ§ΒψCΘ§DΘ§E»ΐΒψ‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§Ν§Ϋ”BDΘ°ΆΦ÷–ΒΡCEΓΔBD”–‘θ―υΒΡ¥σ–ΓΚΆΈΜ÷ΟΙΊœΒΘΩ ‘÷ΛΟςΡψΒΡΫα¬έΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ¥”Τϊ≥ΒΒΤΒΡΒψO¥ΠΖΔ≥ωΒΡ“Μ χΙβœΏΨ≠ΒΤΒΡΖ¥Ιβ’÷Ζ¥…δΚσ―ΊCOΖΫœρΤΫ––…δ≥ωΘ§»γ»κ…δΙβœΏOAΒΡΖ¥…δΙβœΏΈΣABΘ§ΓœOAB=75ΓψΘ°‘Ύ»γΆΦ÷–Υυ ΨΒΡΫΊΟφΡΎΘ§»τ»κ…δΙβœΏODΨ≠Ζ¥Ιβ’÷Ζ¥…δΚσ―ΊDE…δ≥ωΘ§«“ΓœODE=22ΓψΘ°‘ρΓœAODΒΡΕ» ΐ «_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§AΘ®©¹1Θ§5Θ©Θ§BΘ®©¹1Θ§0Θ©Θ§CΘ®©¹4Θ§3Θ©Θ°

Θ®1Θ©‘ΎΆΦ÷–ΒΡΒψ…œ±ξ≥ωœύ”ΠΉ÷ΡΗAΓΔBΓΔCΘ§≤Δ«σ≥ωΓςABCΒΡΟφΜΐΘΜ
Θ®2Θ©‘ΎΆΦ÷–Ής≥ωΓςABCΙΊ”Ύy÷αΒΡΕ‘≥ΤΆΦ–ΈΓςA1B1C1ΘΜ
Θ®3Θ©–¥≥ωΒψA1Θ§B1Θ§C1ΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ «Ρ≥ΙΪ‘Α“Μ‘≤–Έ≈γΥ°≥ΊΘ§Υ°Νς‘ΎΗςΗωΖΫœρ―Ί–ΈΉ¥œύΆ§ΒΡ≈ΉΈοœΏ¬δœ¬Θ§Ϋ®ΝΔ»γœ¬ΆΦΥυ ΨΒΡΉχ±ξœΒΘ§»γΙϊ≈γΆΖΥυ‘Ύ¥ΠA(0,1.25)Θ§Υ°Νς¬ΖœΏΉνΗΏ¥ΠMΘ®1Θ§2.25Θ©Θ§‘ρΗΟ≈ΉΈοΒΡΫβΈω ΫΈΣ__________________________ΓΘ»γΙϊ≤ΜΩΦ¬«ΤδΥϊ“ρΥΊΘ§Ρ«Ο¥Υ°≥ΊΒΡΑκΨΕ÷Ν…Ό“Σ______mΘ§≤≈Ρή Ι≈γ≥ωΒΡΥ°Νς≤Μ÷Ν¬δΒΫ≥ΊΆβ.
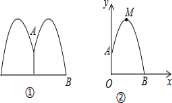
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com