
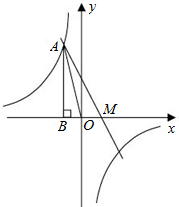
 ��ͼ����֪����������$y=\frac{k}{x}$��ͼ���ڶ������ڵĵ�A��-1��m����AB��x���ڵ�B����AOB�����Ϊ2����ֱ��y=ax+b������A�����Ҿ�������������$y=\frac{k}{x}$��ͼ������һ��C��n��-2����
��ͼ����֪����������$y=\frac{k}{x}$��ͼ���ڶ������ڵĵ�A��-1��m����AB��x���ڵ�B����AOB�����Ϊ2����ֱ��y=ax+b������A�����Ҿ�������������$y=\frac{k}{x}$��ͼ������һ��C��n��-2�������� ��1�����ݵ�A�ĺ��������AOB��������AB�ij��ȣ��Ӷ��õ���A�����꣬Ȼ�����ô���ϵ���������������������ʽ�������÷�������������ʽ�����C�����꣬���ݵ�A���C���������ô���ϵ�����������ֱ��y=ax+b�Ľ���ʽ��
��2������ֱ��y=ax+b�Ľ���ʽ��ȡy=0�������Ӧ��x��ֵ���õ���M�����꣬Ȼ�����BM�ij��ȣ��ڡ�ABM�����ù��ɶ����������AM�ij��ȣ�
��3������S��AOC=S��AOM+S��COM��ü��ɣ�
��� �⣺��1���ߵ�A��-1��m���ڵڶ������ڣ�
��AB=m��OB=1��
��S��ABO=$\frac{1}{2}$AB•BO=2��
����$\frac{1}{2}$��m��1=2��
���m=4��
��A ��-1��4����
�ߵ�A ��-1��4�����ڷ���������$y=\frac{k}{x}$��ͼ���ϣ�
��4=$\frac{k}{-1}$��
���k=-4��
�෴��������Ϊy=-$\frac{4}{x}$��
�֡߷���������y=-$\frac{4}{x}$��ͼ��C��n��-2��
��-2=$\frac{-4}{n}$��
���n=2��
��C ��2��-2����
��ֱ��y=ax+b����A ��-1��4����C ��2��-2��
��$\left\{\begin{array}{l}{4=-a+b}\\{-2=2a+b}\end{array}\right.$��
�ⷽ����� $\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$��
��ֱ��y=ax+b�Ľ���ʽΪy=-2x+2��
��2����y=0ʱ����-2x+2=0��
���x=1��
���M��������M��1��0����
��Rt��ABM��
��AB=4��BM=BO+OM=1+1=2��
�ɹ��ɶ�����AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��
��3��S��AOC=S��AOM+S��COM=$\frac{1}{2}$��1��4+$\frac{1}{2}$��1��2=3��
���� ������Ҫ�����˷�����������һ�κ����Ľ������⣬����ϵ������������ʽ�����ɶ���������������ȣ��������մ���ϵ�����ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
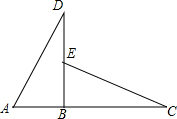 ��ͼ����ABD�ա�EBC��AB=2cm��BC=5cm
��ͼ����ABD�ա�EBC��AB=2cm��BC=5cm�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
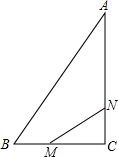 ��ͼ����Rt��ABC�У���C=90�㣬AC=8cm��BC=6cm������M��ÿ��1cm���ٶȴӵ�B���C�ƶ���ͬʱ����N��3cm���ٶȴӵ�C��A�ƶ�������N�����Aʱ�����㶼ֹͣ�ƶ�������MN�����ƶ�ʱ��Ϊt�룮
��ͼ����Rt��ABC�У���C=90�㣬AC=8cm��BC=6cm������M��ÿ��1cm���ٶȴӵ�B���C�ƶ���ͬʱ����N��3cm���ٶȴӵ�C��A�ƶ�������N�����Aʱ�����㶼ֹͣ�ƶ�������MN�����ƶ�ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
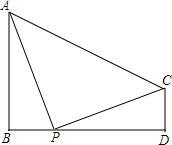 ��ͼ����֪AB�ABD��CD�ABD��
��ͼ����֪AB�ABD��CD�ABD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ��Բ�ָ���ĸ����Σ����ǵ�Բ�ĽǵĶ�����Ϊ2��3��4��3��
��ͼ��ʾ��һ��Բ�ָ���ĸ����Σ����ǵ�Բ�ĽǵĶ�����Ϊ2��3��4��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com