
为了抓住世界杯商机,某商店决定购进A、B两种世界杯纪念品.若购进A种纪念品10件,B种纪念品5件,需要1 000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
(1)50,100;(2)共有6种进货方案;(3)当购进A种纪念品160件,B种纪念品20件时,可获最大利润,最大利润是3800元.
【解析】
试题分析:(1)设我校购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,根据条件建立二元一次方程组求出其解即可;
(2)设我校购进A种纪念品x个,购进B种纪念品y个,根据条件的数量关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=两种商品的利润之和建立解析式,由解析式的性质就可以求出结论.
试题解析::(1)设我校购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,由题意,得
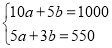 ,
,
∴解方程组得:

答:购进一件A种纪念品需要50元,购进一件B种纪念品需要100元.
(2)设我校购进A种纪念品x个,购进B种纪念品y个,由题意,得
则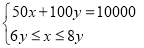 ,
,
解得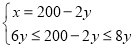 ,
,
解得:20≤y≤25
∵y为正整数
∴y=20,21,22,23,24,25
答:共有6种进货方案;
(3)设总利润为W元,由题意,得
W=20x+30y=20(200-2 y)+30y,
=-10y+4000(20≤y≤25)
∵-10<0,
∴W随y的增大而减小,
∴当y=20时,W有最大值
W最大=-10×20+4000=3800(元)
答:当购进A种纪念品160件,B种纪念品20件时,可获最大利润,最大利润是3800元.
考点:1.一次函数的应用;2.二元一次方程组的应用;3.一元一次不等式组的应用.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
已知二次函数 的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
A.(1,0) B.(-1,0) C.(2,0) D.(-2,0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:解答题
在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB. 设 =k.
=k.
(1)证明:△BGF是等腰三角形;
(2)当k为何值时,△BGF是等边三角形?并说明理由。
(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.
利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )
(A) (B)
(B) (C)
(C)  (D)
(D)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
据统计,1959年南湖革命纪念馆成立以来,约有2500万人次参观了南湖红船(中共一大会址).数2500万用科学计数法表示为( )
(A)2.5×108 (B)2.5×107 (C)2.5×106 (D)25×106
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是

A.4 B.5 C.6 D.10
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值 范围;
(2)设宾馆一天的 利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市中考一模数学试卷(解析版) 题型:选择题
已知点M(1-2m,m-1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
A.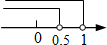 B.
B.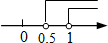 C.
C.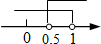 D.
D.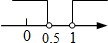
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com