
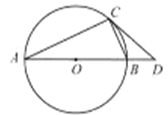
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的延长线交于
的延长线交于![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 半径.
半径.
【答案】(1)证明见解析;(2)⊙O半径是![]() .
.
【解析】
试题分析:(1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.
(2)首先设CD为x,则AB=![]() x,OC=OB=
x,OC=OB=![]() x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:
x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:![]() ,据此求出CB的值是多少,即可求出⊙O半径是多少.
,据此求出CB的值是多少,即可求出⊙O半径是多少.
试题解析:(1)证明:如图,连接CO,
 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB=![]() x,OC=OB=
x,OC=OB=![]() x,
x,
∵∠OCD=90°,
∴OD=![]() ,
,
∴BD=OD﹣OB=![]() ,
,
由(1)知,△ADC∽△CDB,
∴![]() ,
,
即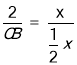 ,
,
解得CB=1,
∴AB=![]() ,
,
∴⊙O半径是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坐标平面上,△ABC≌△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC,若A、B、C的坐标分别为(﹣3,1)、(﹣6,﹣3)、(﹣1,﹣3),D、E两点在y轴上,则F点到y轴的距离为 . 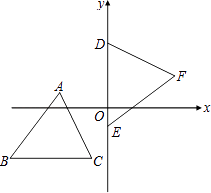
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一次函数y=﹣ ![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
A.(0,3)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(0, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年爆发的世界金融危机,是自上世纪三十年代以来世界最严重的一场金融危机.受金融危机的影响,某商品原价为200元,连续两次降价a%后售价为148元,下面所列方程正确的是( )
A.200(1+a%)2=148
B.200(1﹣a%)2=148
C.200(1﹣2a%)=148
D.200(1﹣a2%)=148
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球的表面积约为510000000km2 , 将510000000用科学记数法表示为( )
A.0.51×109
B.5.1×109
C.5.1×108
D.0.51×107
查看答案和解析>>
科目:初中数学 来源: 题型:
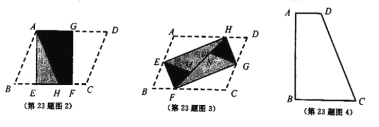
【题目】如图1,将![]() 纸片沿中位线
纸片沿中位线![]() 折叠,使点
折叠,使点![]() 的对称点
的对称点![]() 落在
落在![]() 边上,再将纸片分别沿等腰
边上,再将纸片分别沿等腰![]() 和等腰
和等腰![]() 的底边上的高线
的底边上的高线![]() ,
,![]() 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
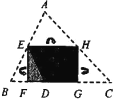
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_____,_____;
,则操作形成的折痕分别是线段_____,_____;![]() ______.
______.
(2)![]() 纸片还可以按图3的方式折叠成一个叠合矩形
纸片还可以按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)如图4,四边形![]() 纸片满足
纸片满足![]() .小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出
.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com