
如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )

A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE= AB
AB
D.S△ABC=3S△DEF
C
【解析】
求出∠BDE=∠FEC=∠AFD=30°,求出∠DEF=∠DFE=∠EDF=60°,推出DF=DE=EF,即可得出等边三角形DEF,根据全等三角形性质推出三个三角形全等即可.求出AB=3BE,DE=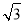 BE,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.
BE,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=∠A=60°,
∵DE⊥BC、EF⊥AC、FD⊥AB,
∴∠DEB=∠EFC=∠FDA=90°,
∴∠BDE=∠FEC=∠AFD=30°,
∴∠DEF=∠DFE=∠EDF=180°﹣90°﹣30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形,
在△ADF、△BED、△CFE中

∴△ADF≌△BED≌△CFE,
∴AD=BE=CF,
∵∠DEB=90°,∠BDE=30°,
∴BD=2BE,DE=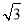 BE,
BE,
∴AB=3BE,
即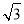 DE=AB,
DE=AB,
即DE=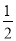 AB错误;
AB错误;
∵△ABC和△DEF是等边三角形,
∴△ABC∽△DEF,
∴S△ABC:S△DEF=(AB)2:(DE)2=(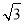 DE)2:DE2=3,
DE)2:DE2=3,
即只有选项C错误;选项A、B、D正确.
故选C.



科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等腰三角形练习卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A.BD=CE B.AD=AE C.DA=DE D.BE=CD
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等边三角形练习卷(解析版) 题型:选择题
如图所示,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F,则∠DFC的度数为( )

A.60° B.45° C.40° D.30°
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等边三角形练习卷(解析版) 题型:选择题
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等边三角形练习卷(解析版) 题型:填空题
已知等边三角形ABC的高为4,在这个三角形所在的平面内有一点P,若点P到AB的距离是1,点P到AC的距离是2,则点P到BC的最小距离和最大距离分别是 .
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级下册第十四章14.3等边三角形练习卷(解析版) 题型:填空题
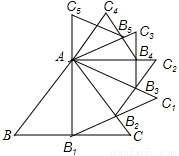
已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学九年级上册第二十四章24.2练习卷(解析版) 题型:选择题
如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )

A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学九年级上册第二十四章24.4练习卷(解析版) 题型:选择题
已知在△ABC中,点D、点E分别在边AB和边AC上,且AD=2DB,AE=2EC, ,
, ,用
,用 、
、 表示向量
表示向量 正确的是( )
正确的是( )
A. B.
B. C.
C.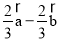 D.
D.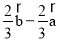
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com