
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.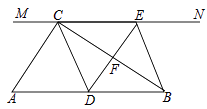
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【答案】
(1)
证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)
解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)
当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
【解析】(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)求出∠CDB=90°,再根据正方形的判定推出即可.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4) ![]() 中正确的有( )
中正确的有( )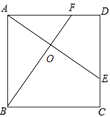
A. 4个
B. 3个
C. 2个
D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )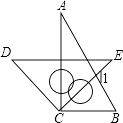
A.75°
B.105°
C.110°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
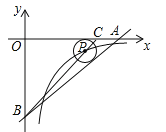
【题目】如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (
(![]() )的图象经过圆心P,则k= .
)的图象经过圆心P,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=°,
∴∠A+∠B+∠C+∠D+∠E=°,
∴∠A=∠B=∠C=∠D=∠E=°.
拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A、∠B、∠C、∠D、∠E的和.
应用:如图③.小明将图②中的点A落在BE上,点C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=°.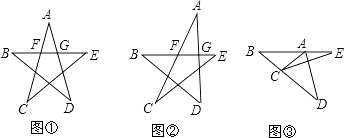
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1 , a2 , a3 , a4…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|…依此类推,则a2017的值为( )
A.﹣1009
B.﹣1008
C.﹣2017
D.﹣2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校师生为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制如下统计表:
零花钱数额/元 | 5 | 10 | 15 | 20 |
学生人数/名 | a | 15 | 20 | 5 |
根据表格中信息,回答下列问题:
(1)求a的值.
(2)求着50名学生每人一周内零花钱数额的中位数.
(3)随机抽查一名学生,抽到一周内零花钱数额不大于10元的同学概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b-6|=0。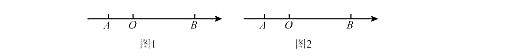
(1)点A表示的数为,点B表示的数为;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=BC,则C点表示的数为;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左动。在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒)。
①分别表示出甲、乙两小球到原点的距离(用t表示)
②求甲、乙两小球到原点的距离相等时经历的时间。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com