
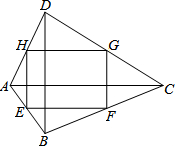
 如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )
如图,四边形ABCD中,AC=8,BD=6,且AC⊥BD,连接四边形ABCD各边中点得到四边形EFGH,下列说法正确的是( )| A. | 四边形EFGH是矩形 | B. | 四边形EFGH的周长是7 | ||
| C. | 四边形EFGH的面积是24 | D. | 四边形ABCD的面积是48 |
分析 利用三角形的中位线定理证得四边形EFGH为平行四边形,然后利用有一个角是直角的平行四边形是矩形可判断选项A是否正确;由AC=8,BD=6,且AC⊥BD,可求出四边形EFGH和ABCD的面积,由此可判断选项CD是否正确;题目给出的数据求不出四边形EFGH的周长,所以选项B错误.
解答 解:
∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形,故选项A正确,符合题意;
∵AC=8,BD=6,且AC⊥BD,
∴四边形ABCD的面积=$\frac{1}{2}$AC•BD=24,故选项D错误,不符合题意;
∵四边形EFGH是矩形,且HG=$\frac{1}{2}$AC=4,HE=$\frac{1}{2}$BD=3
∴四边形EFGH的面积=3×4=12,故选项C错误,不符合题意;
∵EF=$\frac{1}{2}$AC=4,HE=$\frac{1}{2}$BD=3,
∴四边形EFGH的周长=2(3+4)=14,所以选项B错误,不符合题意,
故选A.
点评 本题考查了中点四边形的知识,解题的关键是灵活运用三角形的中位线定理,平行四边形的判断及矩形的判断进行证明,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
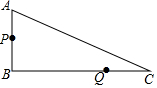 如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.
如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:
所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:| 气质类型 | 频数 | 频率 |
| 胆汁型 | 180 | a |
| 多血质 | 140 | 0.28 |
| 黏液质 | 80 | 0.16 |
| 抑郁质 | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+5(x-12)=48 | B. | x+5(12-x)=48 | C. | 5x+12(x-5)=48 | D. | 5x+(12-x)=48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com