
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定,逐个验证即可.
解答 解:①一组对角相等,一组邻角互补.可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形,此选项正确;
②一组对边平行,另一组对边相等的四边形不是平行四边形,此选项错误;
③由一组对边平行,一组对角相等可得另一组对边平行,所以是平行四边形,此选项正确;
④一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,故本选项错误;
所以①③共2项正确,
故选B.
点评 本题考查平行四边形的判定,注意间接条件的应用.在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.


科目:初中数学 来源: 题型:解答题
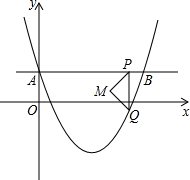 如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
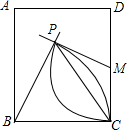 如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )
如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )| A. | 55° | B. | 40° | C. | 35° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y3<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com