
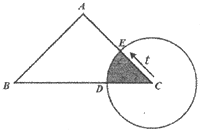
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )
A. 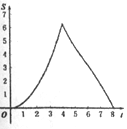 B.
B. 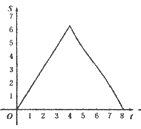
C. 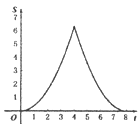 D.
D. 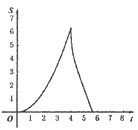
科目:初中数学 来源: 题型:
【题目】问题背景:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的最大值.解决方法:以
的最大值.解决方法:以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,推出
,推出![]() ,当点
,当点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值
取得最大值![]() .
.
问题解决:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() 取得最大值时,
取得最大值时,![]() 的度数为_________.
的度数为_________.
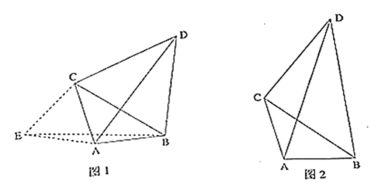
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC的边AB=5,AC=4,BC=3,矩形DEFG的四个顶点都在Rt△ABC的边上,当矩形DEFG的面积最大时,其对角线的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点D,点E是直线AC上一动点,连接DE,过点D作
于点D,点E是直线AC上一动点,连接DE,过点D作![]() ,交直线BC于点F.
,交直线BC于点F.
![]() 探究发现:
探究发现:
如图1,若![]() ,点E在线段AC上,则
,点E在线段AC上,则![]() ______;
______;
![]() 数学思考:
数学思考:
![]() 如图2,若点E在线段AC上,则
如图2,若点E在线段AC上,则![]() ______
______![]() 用含m,n的代数式表示
用含m,n的代数式表示![]() ;
;
![]() 当点E在直线AC上运动时,
当点E在直线AC上运动时,![]() 中的结论是否任然成立?请仅就图3的情形给出证明;
中的结论是否任然成立?请仅就图3的情形给出证明;
![]() 拓展应用:若
拓展应用:若![]() ,
,![]() ,
,![]() ,请直接写出CE的长.
,请直接写出CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区![]() . 已知教学楼外墙长50米,设矩形
. 已知教学楼外墙长50米,设矩形![]() 的边
的边![]() 米,面积为
米,面积为![]() 平方米.
平方米.
(1)请写出活动区面积![]() 与
与![]() 之间的关系式,并指出
之间的关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 为多少米时,活动区的面积最大?最大面积是多少?
为多少米时,活动区的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
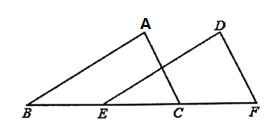
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
解:我写的真命题是:
在![]() 和
和![]() 中,已知:___________________.
中,已知:___________________.
求证:_______________.(不能只填序号)
证明如下:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在锐角三角形ABC中,AB=8,AC=5,BC=6,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,下列结论:①∠CBD=∠EBD,②DE⊥AB,③三角形ADE的周长是7,④![]() ,⑤
,⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
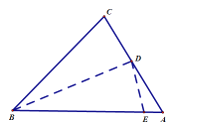
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com