
【题目】Rt△ABC的边AB=5,AC=4,BC=3,矩形DEFG的四个顶点都在Rt△ABC的边上,当矩形DEFG的面积最大时,其对角线的长为_______.
【答案】![]() 或
或![]()
【解析】
分两种情形画出图形分别求解即可解决问题
情况1:如图1中,四边形DEFG是△ABC的内接矩形,设DE=CF=x,则BF=3-x 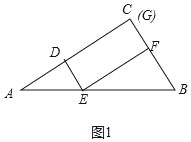
∵EF∥AC,
∴![]() =
=![]()
∴![]() =
=![]()
∴EF=![]() (3-x)
(3-x)
∴S矩形DEFG=x![]() (3-x)=﹣
(3-x)=﹣![]() (x-
(x-![]() )2+3
)2+3
∴x=![]() 时,矩形的面积最大,最大值为3,此时对角线=
时,矩形的面积最大,最大值为3,此时对角线=![]() .
.
情况2:如图2中,四边形DEFG是△ABC的内接矩形,设DE=GF=x,
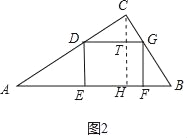
作CH⊥AB于H,交DG于T.则CH=![]() ,CT=
,CT=![]() ﹣x,
﹣x,
∵DG∥AB,
∴△CDG∽△CAB,
∴![]()
∴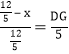
∴DG=5﹣![]() x,
x,
∴S矩形DEFG=x(5﹣![]() x)=﹣
x)=﹣![]() (x﹣
(x﹣![]() )2+3,
)2+3,
∴x=![]() 时,矩形的面积最大为3,此时对角线=
时,矩形的面积最大为3,此时对角线=![]() =
=![]()
∴矩形面积的最大值为3,此时对角线的长为![]() 或
或![]()
故答案为![]() 或
或![]()


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,BE与CD交与点O,给出下列四个条件:①∠DBO=∠ECO,②∠BDO=∠CEO,③BD=CE,④OB=OC.

(1)从上述四个条件中,任选两个为条件,可以判定△ABC是等腰三角形?写出所有可能的情况.
(2)选择(1)中的某一种情形,进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)判断线段AB与OC 的位置关系是什么?并说明理由;
(3)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=24,DE=17.
(1)求证:△CAD≌△CBE;
(2)求线段AB的长度.
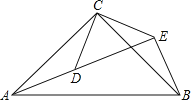
查看答案和解析>>
科目:初中数学 来源: 题型:
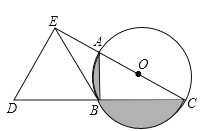
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
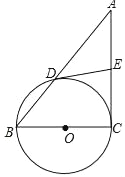
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AB=25,DE=10,弧DC的长为a,求DE、EC和弧DC围成的部分的面积S.(用含字母a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
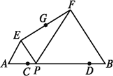
【题目】如图所示,已知AB= 6,点C,D在线段AB上,AC =DB = 1,P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G,当点P从点C运动到点D时,则点G移动路径的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
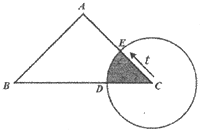
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )
A. 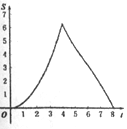 B.
B. 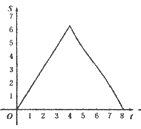
C. 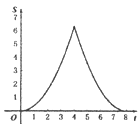 D.
D. 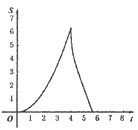
查看答案和解析>>
科目:初中数学 来源: 题型:
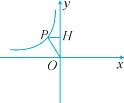
【题目】如图是反比例函数y=![]() 的图象的一支.
的图象的一支.
(1)求m的取值范围,并在图中画出另一支的图象;
(2)若m=-1,P(a,3)是双曲线上的一点,PH⊥y轴于H,将线段OP向右平移3PH的长度至O′P′,此时P的对应点P′恰好在另一条双曲线y=![]() 的图象上,则平移中线段OP扫过的面积为 ,k= .
的图象上,则平移中线段OP扫过的面积为 ,k= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com