
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)判断线段AB与OC 的位置关系是什么?并说明理由;
(3)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,CD=2,点P′是AB上的动点,则PC+PD的最小值是( )
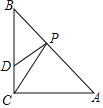
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
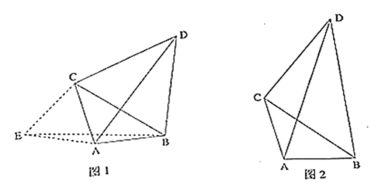
【题目】问题背景:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的最大值.解决方法:以
的最大值.解决方法:以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,推出
,推出![]() ,当点
,当点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值
取得最大值![]() .
.
问题解决:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() 取得最大值时,
取得最大值时,![]() 的度数为_________.
的度数为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
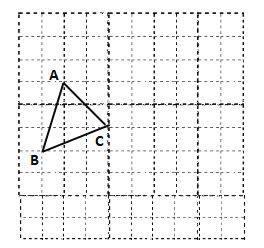
【题目】如图,在边长为1的小正方形组成的10×10网络中(我们把组成网格的小正方形的顶点称为格点),△ABC的三个顶点分别在网格的格点上
(1)请你在所给的网格中建立平面直角坐标系,使△ABC的顶点A的坐标为(-3,5);
(2)在(1)的坐标系中,直接写出△ABC其它两个顶点的坐标;
(3)在(1)的坐标系中,画出△ABC关于y轴对称的图形△A1B1C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面真角坐标系中,点A.B的坐标分别为A(a,0),B(b,0),且a,b满足|a+1|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM=![]() S△ABC,试求点M的坐标.
S△ABC,试求点M的坐标.
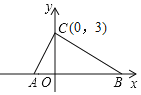
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC的边AB=5,AC=4,BC=3,矩形DEFG的四个顶点都在Rt△ABC的边上,当矩形DEFG的面积最大时,其对角线的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明.
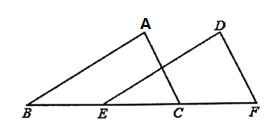
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
解:我写的真命题是:
在![]() 和
和![]() 中,已知:___________________.
中,已知:___________________.
求证:_______________.(不能只填序号)
证明如下:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com