
【题目】如图所示,在平面真角坐标系中,点A.B的坐标分别为A(a,0),B(b,0),且a,b满足|a+1|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM=![]() S△ABC,试求点M的坐标.
S△ABC,试求点M的坐标.
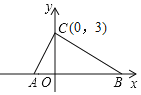
【答案】(1)a=﹣1,b=5,S△ABC=9;(2)M的坐标为(1,0)或(﹣3,0)
【解析】
(1)由|a+1|+![]() =0结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;
=0结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;
(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM=![]() S△ABC,即可得出点M的坐标.
S△ABC,即可得出点M的坐标.
解:(1)由|a+1|+![]() =0,|a+1|≥0,
=0,|a+1|≥0,![]() ≥0
≥0
∴a+1=0,b﹣5=0,
∴a=﹣1,b=5,
∴点A(﹣1,0),点B(5,0).
又∵点C(0,3),
∴AB=|﹣1﹣5|=6,CO=3,
∴S△ABC=![]() ABCO=
ABCO=![]() ×6×3=9.
×6×3=9.
(2)设点M的坐标为(x,0),则AM=|x﹣(﹣1)|=|x+1|,
又∵S△ACM=![]() S△ABC,
S△ABC,
∴![]() AMOC=
AMOC=![]() ×9,
×9,
∴![]() |x+1|×3=3,
|x+1|×3=3,
∴|x+1|=2,
即x+1=±2,
解得:x=1或﹣3,
故点M的坐标为(1,0)或(﹣3,0).


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
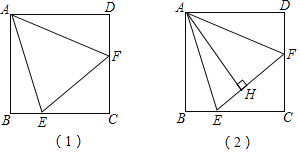
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省攀枝花市)某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)判断线段AB与OC 的位置关系是什么?并说明理由;
(3)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
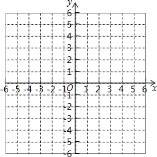
【题目】如图,在平面直角坐标系中,O为坐标原点,点A(4,1),B(1,1)C(4,5),D(6,﹣3),E(﹣2,5)
(1)在坐标系中描出各点,画出△AEC,△BCD.
(2)求出△AEC的面积(简要写明简答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
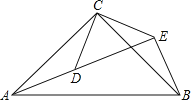
【题目】如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=24,DE=17.
(1)求证:△CAD≌△CBE;
(2)求线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
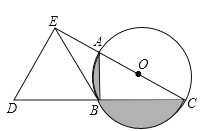
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
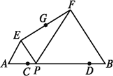
【题目】如图所示,已知AB= 6,点C,D在线段AB上,AC =DB = 1,P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G,当点P从点C运动到点D时,则点G移动路径的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
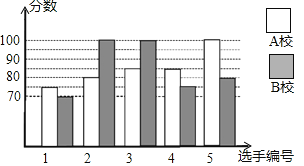
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com