
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,CD=2,点P′是AB上的动点,则PC+PD的最小值是( )
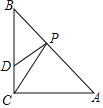
A.7B.8C.9D.10
科目:初中数学 来源: 题型:
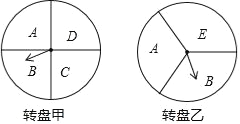
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向 A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二: 同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受 9 折优惠的概率为_______;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
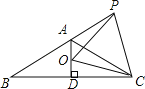
【题目】如图,已知等腰△ABC,∠BAC=120°,AD⊥BC于D点,点P为BA延长线上一点,点O是线段AD上一点,若AC=AO+AP.
(1)求证:∠APO=∠OCA;
(2)求证:△OCP是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
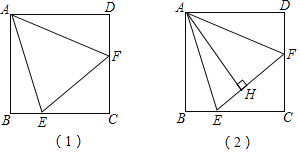
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,BE与CD交与点O,给出下列四个条件:①∠DBO=∠ECO,②∠BDO=∠CEO,③BD=CE,④OB=OC.

(1)从上述四个条件中,任选两个为条件,可以判定△ABC是等腰三角形?写出所有可能的情况.
(2)选择(1)中的某一种情形,进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)判断线段AB与OC 的位置关系是什么?并说明理由;
(3)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com