
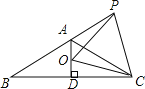
【题目】如图,已知等腰△ABC,∠BAC=120°,AD⊥BC于D点,点P为BA延长线上一点,点O是线段AD上一点,若AC=AO+AP.
(1)求证:∠APO=∠OCA;
(2)求证:△OCP是等边三角形.
【答案】(1)见解析;(2)见解析
【解析】
(1)在AC上截取AE=AP,连接PE,证出△APE是等边三角形,得出∠PEA=∠APE=∠PAE =60°,PE=AP=AE,证出AO=EC,证明△OPA≌△CPE,得出∠APO=∠EPC,OP=CP,证明△OCP是等边三角形,得出∠OCP=60°,即∠OCA+∠PCE=60°,证出∠OCA=∠EPC,即可得出结论;
(2)由(1)得出△OPA≌△CPE,得出∠APO=∠EPC,OP=CP,证出∠OPC=60°,即可得出△OCP是等边三角形.
(1)证明:在AC上截取AE=AP,连接PE,
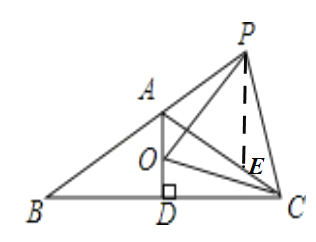
∵∠BAC=120°,AD⊥BC
![]()
![]()
∵∠PAE=180°﹣∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=∠PAE=60°,PE=AP=AE,
∴∠PEC=120°,![]() ,
,
∵AC=AO+AP,AC=AE+EC,
∴AO=EC,
在△OPA和△CPE中,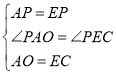 ,
,
∴△OPA≌△CPE(SAS),
∴∠APO=∠EPC,OP=CP,
∴∠OPC=∠OPE+∠EPC=∠OPE+∠APO=∠APE=60°,
∴△OCP是等边三角形,
∴∠OCP=60°,即∠OCA+∠PCE=60°,
∵∠EPC+∠PCE=∠AEP=60°,
∴∠OCA=∠EPC,
∴∠APO=∠OCA;
(2)证明:由(1)得:△OPA≌△CPE(SAS),
∴∠APO=∠EPC,OP=CP,
∴∠OPC=∠OPE+∠EPC=∠OPE+∠APO=∠APE=60°,
∴△OCP是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
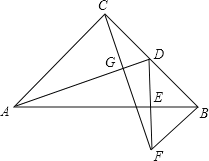
(1)求证:CD=BF;
(2)求证:AD⊥CF;
(3)连接AF,试判断△ACF的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,CD=2,点P′是AB上的动点,则PC+PD的最小值是( )
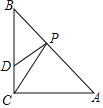
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…,由此可发现:![]() ,
,![]() ,
,![]() ,…,请写出第6个数组:__.
,…,请写出第6个数组:__.
查看答案和解析>>
科目:初中数学 来源: 题型:
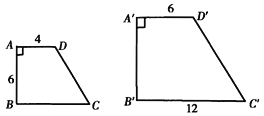
【题目】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
(1)梯形ABCD与梯形A′B′C′D′的相似比k;
(2)A′B′和BC的长;
(3)D′C′∶DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
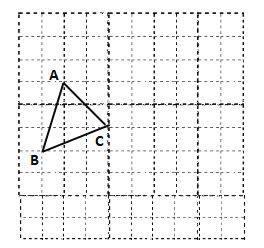
【题目】如图,在边长为1的小正方形组成的10×10网络中(我们把组成网格的小正方形的顶点称为格点),△ABC的三个顶点分别在网格的格点上
(1)请你在所给的网格中建立平面直角坐标系,使△ABC的顶点A的坐标为(-3,5);
(2)在(1)的坐标系中,直接写出△ABC其它两个顶点的坐标;
(3)在(1)的坐标系中,画出△ABC关于y轴对称的图形△A1B1C1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com