练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】四边形ABCD是正方形，AC是对角线，E是平面内一点，且，过点C作，且。连接AE、AF，M是AF的中点，作射线DM交AE于点N.

    （1）如图1，若点E，F分别在BC，CD边上。

    求证：①；

    ②；

    （2）如图2，若点E在四边形ABCD内，点F在直线BC的上方，求与的和的度数。

    【答案】（1）①见解析；②见解析；（2）

    【解析】

    （1）根据已知及正方形的性质，全等三角形的判定，全等三角形的性质的计算，可知①∠BAE＝∠DAF是否成立；可知②DN⊥AE是否成立；

    （2）根据已知及正方形的性质，全等三角形的判定，全等三角形的性质的计算，求出∠EAC与∠ADN的和的度数.

    （1）证明：①在正方形ABCD中，

    ∴，.

    ∵，

    ∴.

    ∴.

    ∴.

    ②∵M是AF的中点，

    ∴，

    由①可知.

    ∵.

    ∵

    ∴

    ∴

    （2）解：延长AD至H，使得，连结FH，CH.

    ∵，

    ∴.

    在正方形ABCD屮，AC是对角线，

    ∴.

    ∴.

    ∴.

    ∴

    又∵，

    p>∴.

    ∴

    ∵M是AF的中点，D是AH的中点，

    ∴.

    ∴

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

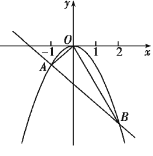
    【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A.B两点,如图所示,其中A(-1,-1).

    (1)求二次函数和一次函数的解析式;

    (2)求△OAB的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=﹣x+2分别交y轴、x轴于A，B两点，抛物线y=﹣x2+bx+c过A，B两点．

    （1）求这个抛物线的解析式；

    （2）作垂直于x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，△NAB的面积有最大值？最大值是多少？

    （3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，折叠矩形ABCD的一边AD，使点D落在BC边上的点F处，已知AB=8，BC=10，

    （1）求BF的长；

    （2）求△ECF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学兴趣小组几名同学到商场调查发现，一种纯牛奶进价为每箱40元，厂家要求售价在40～70元之间，若以每箱70元销售平均每天销售30箱，价格每降低1元平均每天可多销售3箱．

    （1）现该商场要保证每天盈利900元，同时又要使顾客得到实惠，那么每箱售价为多少元？

    （2）若每天盈利为W元，请利用配方法直接写出每箱售价为多少元时，每天盈利最多．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是用长度相等的小棒按一定规律摆成的一组图案

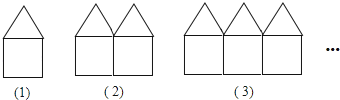
    （1）填写下表：

    图形序号

    ①

    ②

    ③

    ……

    ⑧

    每个图案中小棒的数量

    6

    11

    ……

    （2）请填写出第个图案中小棒的数量（用含的代数式表示）；

    （3）第30个图案中小棒有多少根？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一位农民带上若干千克自产的苹果进城出售.为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的苹果（千克）与他手中持有的钱数（元）（含备用零钱）的关系如图，结合图象解决下列问题：

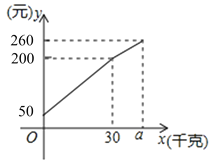
    （1）农民自带的零钱是多少？

    （2）求出降价前每千克的苹果价格是多少？

    （3）降价后他按每千克元将剩余苹果售完，这时他手中的钱（含备用零钱）是元，试求出图象中的值；

    （4）求出降价前与之间的关系式（不要求写的取值范围）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴、y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点P作PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）

    （1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；

    （2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；

    （3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥FC，D是AB上一点，DF交AC于点E，DE=FE，分别延长FD和CB交于点G．

    （1）求证：△ADE≌△CFE；

    （2）若GB=2，BC=4，BD=1，求AB的长．

    查看答案和解析>>

    同步练习册答案