
【题目】数学兴趣小组几名同学到商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.
(1)现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?
(2)若每天盈利为W元,请利用配方法直接写出每箱售价为多少元时,每天盈利最多.
【答案】(1)当每箱牛奶售价为50元时,平均每天的利润为900元.(2)60元.
【解析】
(1)根据平均每天销售这种牛奶的利润=每箱的利润×销售量,设每箱售价为x元,根据“每天盈利900元”列出方程(x-40)[30+3(70-x)]=900 求解即可;
(2)根据平均每天销售这种牛奶的利润等于每箱的利润×销售量得到W=(x-40)[30+3(70-x)],整理后根据二次函数的性质求解.
(1)解:设每箱售价为x元,根据题意得:
(x-40)[30+3(70-x)]=900
化简得:![]() -120x+3500=0
-120x+3500=0
解得:x1=50或x2=70(不合题意,舍去)
∴x=50
答:当每箱牛奶售价为50元时,平均每天的利润为900元.
(2)由题意得W=(x-40)[30+3(70-x)]
=-3![]() +360x-9600
+360x-9600
![]()
∴当售价为每箱牛奶60元时,每天盈利最多.


科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(2x+3)2-16=0;
(2)(x-2)2-3x(x-2)=0.
(3)x2+4x=2
(4)x(x+4)=8x+12
查看答案和解析>>
科目:初中数学 来源: 题型:
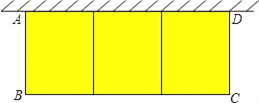
【题目】如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是边BC上的中线,AE∥BC,DE∥AB,DE与AC交于点O,连接CE.
(1)求证:AD=EC;
(2)若∠BAC=90°,求证:四边形ADCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.旨在借用古代丝绸之路的历史符号,高举和平发展的旗帜,积极发展与沿线国家的经济合作.2018年底共开行中欧班列6300列,其中返程班列2690列,实现进出口贸易总额170亿美元.数据170亿用科学计数法表示为![]() ,则
,则![]() 的值为( )
的值为( )
A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且![]() ,过点C作
,过点C作![]() ,且
,且![]() 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
(1)如图1,若点E,F分别在BC,CD边上。
求证:①![]() ;
;
②![]() ;
;
(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求![]() 与
与![]() 的和的度数。
的和的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有两个点![]() ,
,![]() .
.
(1)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(2)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(3)若![]() 、
、![]() 两点重合,将重合后的点绕原点顺时针旋转
两点重合,将重合后的点绕原点顺时针旋转![]() ,此时点的坐标为__________.
,此时点的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为![]() x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )

A.6B.3![]() -3C.3
-3C.3![]() -2D.3
-2D.3![]() -
-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com