
【题目】如图,在△ABC中,AD是边BC上的中线,AE∥BC,DE∥AB,DE与AC交于点O,连接CE.
(1)求证:AD=EC;
(2)若∠BAC=90°,求证:四边形ADCE是菱形.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)求△DOC的面积.
(3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=![]() x2﹣
x2﹣![]() x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D

(1)求出点A,B,D的坐标;
(2)如图1,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′.首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当△CMN是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣![]() x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,△NAB的面积有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组几名同学到商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.
(1)现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?
(2)若每天盈利为W元,请利用配方法直接写出每箱售价为多少元时,每天盈利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位农民带上若干千克自产的苹果进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的苹果![]() (千克)与他手中持有的钱数
(千克)与他手中持有的钱数![]() (元)(含备用零钱)的关系如图,结合图象解决下列问题:
(元)(含备用零钱)的关系如图,结合图象解决下列问题:
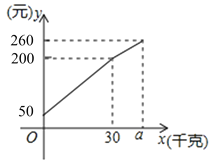
(1)农民自带的零钱是多少?
(2)求出降价前每千克的苹果价格是多少?
(3)降价后他按每千克![]() 元将剩余苹果售完,这时他手中
元将剩余苹果售完,这时他手中![]() 的钱(含备用零钱)是
的钱(含备用零钱)是![]() 元,试求出图象中
元,试求出图象中![]() 的值;
的值;
(4)求出降价前![]() 与
与![]() 之间的关系式(不要求写
之间的关系式(不要求写![]() 的取值范围).
的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.
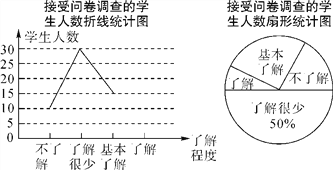
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com