
【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A.B两点,如图所示,其中A(-1,-1).
(1)求二次函数和一次函数的解析式;
(2)求△OAB的面积.
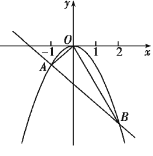
【答案】(1)y=-x2;(2)3
【解析】
(1)利用点A的坐标可求出直线与抛物线的解析式;
(2)求出点G的坐标及点B的坐标,利用S△OAB=![]() OG|A的横坐标|+
OG|A的横坐标|+![]() OG点B的横坐标求解即可.
OG点B的横坐标求解即可.
(1)∵一次函数y=kx-2的图象过点A(-1,-1),
∴-1=-k-2,解得k=-1,
∴一次函数的解析式为y=-x-2.
∵y=ax2过点A(-1,-1),
∴-1=a×(-1)2,解得a=-1,
∴二次函数的解析式为y=-x2.
(2)设AB交y轴于点G,过B作BH⊥OG于点H.
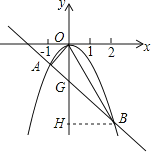
在y=-x-2中,令x=0,得y=-2,
∴G(0,-2),
联立一次函数与二次函数解析式可得![]()
解得![]() 或
或![]()
∴B(2,-4),∴BH=2.
∴S△OAB=S△AOG+S△BOG=![]() ×2×1+
×2×1+![]() ×2×2=1+2=3.
×2×2=1+2=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某种产品形状是长方体,长为8cm,它的展开图如图:
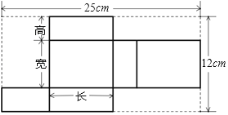
(1)求该长方体的宽和高;
(2)请为厂家设计一种包装纸箱,使每箱能装2件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小),并求出该纸箱的体积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价贵12元,用12000元购进的科普书本数是用9000元购进的文学书本数的![]() .那么文学书和科普书的单价各是多少元?
.那么文学书和科普书的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数按要求分类
+8.3,-4,-0.8,-![]() ,0,π,90,-|-24|,15%,
,0,π,90,-|-24|,15%,![]() 中,
中,
负数有______________________________,
分数有______________________________.
整数有______________________________.
有理数有______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(2x+3)2-16=0;
(2)(x-2)2-3x(x-2)=0.
(3)x2+4x=2
(4)x(x+4)=8x+12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东莞市出租车收费标准如下表所示,根据此收费标准,解决下列问题:
行驶路程 | 收费标准 |
不超出 | 起步价8元 |
超出 | 2.6元/ |
(1)若行驶路程为![]() ,则打车费用为______元;
,则打车费用为______元;
(2)若行驶路程为![]() ,则打车费用为______元(用含
,则打车费用为______元(用含![]() 的代数式表示);
的代数式表示);
(3)某同学周末放学回家,已知打车费用为34元,则他家离学校多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.线段DC上有一点E,当△ABE的面积等于5时,点E的坐标为 .
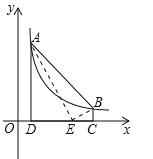
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且![]() ,过点C作
,过点C作![]() ,且
,且![]() 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
(1)如图1,若点E,F分别在BC,CD边上。
求证:①![]() ;
;
②![]() ;
;
(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求![]() 与
与![]() 的和的度数。
的和的度数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com