
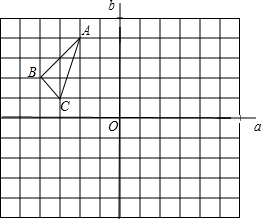
 在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)
在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母) 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知y是x的反比例函数,且当x=4,y=-1.
已知y是x的反比例函数,且当x=4,y=-1.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
|
| 12a |
| 3a |
|
|
| 12 |
|
|
| 2 |
| 3 |
| 9x |
|
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
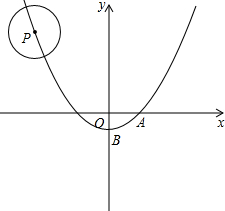 如图,⊙P的半径为r,圆心P在抛物线y=ax2+c上运动.抛物线与x轴和y轴分别交与点A(1,0)点B(0,-1).
如图,⊙P的半径为r,圆心P在抛物线y=ax2+c上运动.抛物线与x轴和y轴分别交与点A(1,0)点B(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:
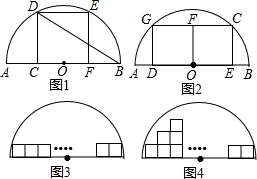 正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现:
正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com