【题目】如图①有一个宝塔，它的地基边缘是周长为26m的正五边形ABCDE（如图②），点O为中心．（下列各题结果精确到0.1m）
（1）求地基的中心到边缘的距离；
（2）己知塔的墙体宽为1m，现要在塔的底层中心建一圆形底座的塑像，并且留出最窄处为1.6m的观光通道，问塑像底座的半径最大是多少？
【答案】（1）3.6m；（2）1m.
【解析】试题分析：（1）构造一个由正多边形的边心距、半边和半径组成的直角三角形．根据正五边形的性质得到半边所对的角是
=36°，再根据题意中的周长求得该正五边形的半边是26÷10=2.6，最后由该角的正切值进行求解；
（2）根据（1）中的结论、塔的墙体宽为1m和最窄处为1.6m的观光通道，进行计算．
试题解析：（1）作OM⊥AB于点M，连接OA、OB，则OM为边心距，∠AOB是中心角．
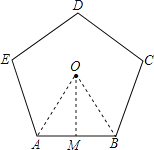
由正五边形性质得∠AOB=360°÷5=72°．
又AB=
×26=5.2，
∴AM=2.6，∠AOM=36°，
在Rt△AMO中，边心距OM=
（2）3.6-1-1.6=1（m）．
答：地基的中心到边缘的距离约为3.6m，塑像底座的半径最大约为1m．
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】小明与小红开展读书比赛．小明找出了一本以前已读完84页的古典名著打算继续往下读，小红上个周末恰好刚买了同一版本的这本名著，不过还没开始读．于是，两人开始了读书比赛．他们利用下表来记录了两人5天的读书进程．
例如，第5天结束时，小明还领先小红24页，此时两人所读到位置的页码之和为424．已知两人各自每天所读页数相同．
（1）表中空白部分从左到右2个数据依次为____，_____；
（2）小明、小红每人每天各读多少页？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，线段
和射线
交于点
．
（
）利用尺规完成以下作图，并保留作图痕迹（不写作法）．
①在射线
上作一点
，使
，连接
；
②作
的角平分线交
于
点；
③在射线
上作一点
，使
，连接
．
（
）在（
）所作的图形中，通过观察和测量可以发现
，请将下面的证明过程补充完整．
证明：∵
，
∴
__________
__________，①
∵
平分
，
∴
，
∴
__________，②
∵
，
∴
，
∵
，
∴
，
∴
，
∴
．（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知锐角三角形ABC内接于⊙O，AD⊥BC，垂足为D．
（1）如图1， 
，BD＝DC，求∠B的度数；
（2）如图2，BE⊥AC，垂足为E，BE交AD于点F，过点B作BG∥AD交⊙O于点G，在AB边上取一点H，使得AH＝BG．求证：△AFH是等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，AD是BC边上的中线.
(1)画出与△ACD关于点D成中心对称的三角形；
(2)找出与AC相等的线段；
(3)探究：△ABC中AB与AC的和与中线AD之间有何大小关系？并说明理由；
(4)若AB=5，AC=3，求线段AD的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，是交警在一个路口统计的某个时段来往车辆的车速(单位：km/h)．
（1）计算这些车的平均速度．
（2）车速的众数是多少？
（3）车速的中位数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
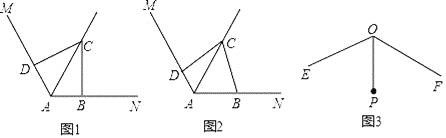
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD= °，△CBD是 三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有 ．（只填序号）
①2个②3个③4个④4个以上
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如右图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．
（1）请在图中画出平移后的△ABC，
（2）再在图中画出△ABC的高CD，
（3）在右图中能使S△ABC=S△PBC的格点P的个数有 个(点P异于A)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
