

分析 (1)如图1,先根据题意得:AM=t,CN=2t,把t=2代入得,AM=2,CN=2t=4,由菱形对边平行计算出∠DCA=30°,根据30°的三角函数求出QN的长;
(2)分两种情况:
①当0≤t≤4时,如图2,过Q作QE⊥AB于E,连接BD交AC于O,先根据勾股定理求OC的长,由三角函数表示出CQ和AQ的长,则可以得出△AMQ的高QE的长,代入面积公式列等式可求出t的值;
②当4<t≤8时,如图3,延长NQ交AB于E,过B作BF⊥CD于F,则NE⊥AB,先求CH和BF的长,所以再求QE的长,代入面积公式列等式可求出t的值;
(3)当△AMQ为等腰三角形,分AM=MQ或AQ=QM或QA=AM三种情况讨论;分别计算对应t的值.
解答 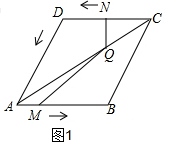 解:(1)如图1,由题意得:AM=t,CN=2t,
解:(1)如图1,由题意得:AM=t,CN=2t,
当t=2时,AM=2,CN=2t=4,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DCB+∠D=180°,
∵∠D=120°,
∴∠DCB=60°,
∵AC平分∠DCB,
∴∠DCA=$\frac{1}{2}$∠DCB=30°,
在Rt△CNQ中,tan∠DCA=$\frac{NQ}{NC}$,
NQ=NC•tan∠DCA=4×tan30°=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$;
(2)分两种情况:
①当0≤t≤4时,如图2,过Q作QE⊥AB于E,连接BD交AC于O,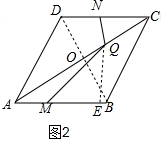
∵四边形ABCD为菱形,
∴AD=AB=8,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴BD=8,
∴OB=4,
∴OC=$\sqrt{D{C}^{2}-O{D}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴AC=8$\sqrt{3}$,
∵DC∥AB,
∴∠BAC=∠DCA=30°,
在Rt△NQC中,CN=2t,
cos30°=$\frac{CN}{CQ}$,
CQ=$\frac{2t}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}t}{3}$,
∴AQ=AC-CQ=8$\sqrt{3}$-$\frac{4\sqrt{3}t}{3}$,
∴QE=$\frac{1}{2}$AQ=$\frac{1}{2}$(8$\sqrt{3}$-$\frac{4\sqrt{3}t}{3}$),
S△AMQ=$\frac{1}{2}$AM•EQ=$\sqrt{3}$,
∴t•$\frac{1}{2}$(8$\sqrt{3}$-$\frac{4\sqrt{3}t}{3}$)=2$\sqrt{3}$,
解得:t1=3+$\sqrt{6}$>4(不符合题意,舍),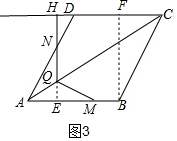 t2=3-$\sqrt{6}$;
t2=3-$\sqrt{6}$;
②当4<t≤8时,如图3,延长NQ交AB于E,过B作BF⊥CD于F,则NE⊥AB,
∵CD+DN=2t,CD=8,
∴DN=2t-8,
∵∠ADC=120°,
∴∠HDN=60°,
在Rt△DHN中,∠HND=30°,
∴DH=$\frac{1}{2}$DN=t-4,
∴CH=CD+DH=8+t-4=t+4,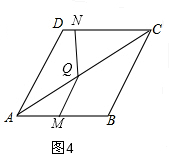
在Rt△CHQ中,tan∠DCA=$\frac{HQ}{CH}$,
∴HQ=CH•tan30°=$\frac{\sqrt{3}}{3}$(t+4),
在Rt△BFC中,∠FBC=30°,BC=8,
∴CF=4,
∴BF=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴QE=4$\sqrt{3}$-$\frac{\sqrt{3}}{3}$(t+4),
∴AQ=2QE=$\frac{16\sqrt{3}}{3}$-$\frac{2\sqrt{3}}{3}$t,
S△AMQ=$\frac{1}{2}$AM•QE=$\sqrt{3}$,
则t•[4$\sqrt{3}$-$\frac{\sqrt{3}}{3}$(t+4)]=2$\sqrt{3}$,
解得:t1=4+$\sqrt{10}$,t2=4-$\sqrt{10}$<4(不符合题意,舍);
综上所述,当△AMQ的面积为$\sqrt{3}$时,t的值为3-$\sqrt{6}$或4+$\sqrt{10}$;
(3)当△AMQ为等腰三角形,则AM=MQ或AQ=QM或QA=AM,
①当AM=MQ时,如图4,
∴∠CAB=∠AQM=30°,
∴∠ACB=∠AQM=30°,
∴△AMQ∽△ABC,得$\frac{AQ}{AC}=\frac{AM}{AB}$,
代入AQ=8$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t,解得t=$\frac{24}{7}$,符合0≤t≤4,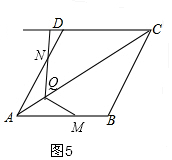
代入AQ=$\frac{16\sqrt{3}}{3}$-$\frac{2\sqrt{3}}{3}$t,解得t=$\frac{16}{5}$,不符合4<t≤8,舍去,
②当AQ=QM时,如图5,有△AMQ∽△ACB,得$\frac{AQ}{AB}=\frac{AM}{AC}$,
代入AQ=8$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t,解得t=$\frac{24}{7}$,不符合0≤t≤4,舍去,
代入AQ=$\frac{16\sqrt{3}}{3}$-$\frac{2\sqrt{3}}{3}$t,解得t=$\frac{16}{3}$,符合4<t≤8,
③当QA=AM时,
代入AQ=8$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$t,解得t=$\frac{(4-\sqrt{3})×24}{13}$,不符合0≤t≤4,舍去,
代入AQ=$\frac{16\sqrt{3}}{3}$-$\frac{2\sqrt{3}}{3}$t,解得t=16(2-$\sqrt{3}$)=32-16$\sqrt{3}$,符合4<t≤8,
综上所述,当t=$\frac{24}{7}$或$\frac{16}{3}$或32-16$\sqrt{3}$时,△AMQ为等腰三角形.
点评 本题是菱形和动点的综合题,考查了菱形、等腰三角形的性质,对于动点问题,要弄清动点的速度、时间、路程及行动路线,本题要首先表示两动点M、N的路程,要注意动点N在线段DC上和AD上时,所构成的△AQM的面积的不同;对于第三问中的等腰三角形的问题,属于常考题型,要分三种情况进行讨论,根据腰的不同、时间的不同,列式代入计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
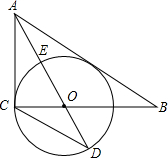 如图,在Rt△ABC中,∠ACB=90°,AO是∠ABC的角平分线,以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是∠ABC的角平分线,以O为圆心,OC为半径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com