
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.

(1)求证:![]() 为等腰三角形;
为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2) E点坐标为![]() ;(3)存在三点,
;(3)存在三点,![]() ,
,![]() ,
,![]()
【解析】
(1)分析题目,证明OD=BD即可证明![]() 为等腰三角形,根据折叠的性质即可得到;
为等腰三角形,根据折叠的性质即可得到;
(2)根据矩形的性质先把OD的长度计算出来,再证明DE=CD,根据面积公式即可得到答案;
(3)分情况讨论点F所在的象限,根据平行四边形的性质计算即可得到.
解:(1)∵![]() 是由
是由![]() 折叠所得,
折叠所得,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
又∵四边形OABC是矩形,
∴OA∥BC,
∴![]() ,
,
∴OD=BD
∴![]() 为等腰三角形
为等腰三角形
(2)过点E作EF⊥![]() 轴于F交BC于G,设CD的长为
轴于F交BC于G,设CD的长为![]() ,则BD=BC-CD=8-
,则BD=BC-CD=8-![]() ,由(1)知OD=BD=8-
,由(1)知OD=BD=8-![]() ,
,
∵四边形ABCD是矩形,,
∴∠OCD=∠OAB=90°,CA=AB,
∴在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,即CD=3,OD=BD=8-
,即CD=3,OD=BD=8-![]() =5,
=5,
由(1)知,![]() ≌
≌![]() ,
,
∴∠OEB=∠OAB=90°
∴∠OCD=∠BED=90°,
在![]() 和
和![]() 中,
中,
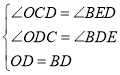 ,
,
∴![]() ≌
≌![]() (AAS),
(AAS),
∴DE=CD=3 ,BE=OC=4,
∵EF⊥![]() 轴,
轴,
∴∠OFB=90°,
∵OA∥BC,
∴∠CGE=∠OFB=90°,
∴CG⊥BD,
∴![]() ,
,
即![]() ,
,
∴在![]() 中,
中,![]() ,
,
∵∠OCG=∠OFE=∠CGF =90°,
∴四边形OFGC是矩形,
∴OF=CG=CD+DG=3+![]() =
=![]() ,
,
∴EF=GE+GF=![]() +4=
+4=![]() ,
,
故E点坐标为![]() ;
;
(3) 存在三点![]() ,
,![]() ,
,![]()
(附答案)可分三种情况:
1.点F在第二象限,如图1:
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ;
;
2.点F在第四象限,如图2:
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ;
;
3.点F在第一象限,如图3:
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ;
;
故存在三点![]() ,
,![]() ,
,![]() 使得以点B,E,F,O为顶点的四边形是平行四边形.
使得以点B,E,F,O为顶点的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是三角形纸片
是三角形纸片![]() 的高,将纸片沿直线
的高,将纸片沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,给出下列判断:
重合,给出下列判断:

①![]() 是
是![]() 的中位线;
的中位线;
②![]() 的周长等于
的周长等于![]() 周长的一半:
周长的一半:
③若四边形![]() 是菱形,则
是菱形,则![]() ;
;
④若![]() 是直角,则四边形
是直角,则四边形![]() 是矩形.
是矩形.
其中正确的是( )
A.①②③B.①②④C.②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车早晨7∶00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B、C、D在同一条直线上),小明研究图像得到了以下结论:
①甲乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8∶00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8∶24,
其中,正确的结论是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由![]() 两工程队先后接力完成.
两工程队先后接力完成.![]() 工作队每天整治12米,
工作队每天整治12米,![]() 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
![]()
![]()
![]()
![]() 甲:
甲: ![]() 乙:
乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数![]() 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:![]() 表示________________,
表示________________,![]() 表示_______________;
表示_______________;
乙:![]() 表示________________,
表示________________,![]() 表示_______________.
表示_______________.
(2)求![]() 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
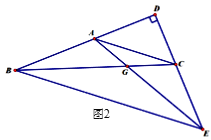
【题目】已知:如图,![]() ABC中,CD⊥BA交BA延长线于点D,∠ABC=∠ACB
ABC中,CD⊥BA交BA延长线于点D,∠ABC=∠ACB
(1)求证:∠DCB=![]() ∠BAC.
∠BAC.
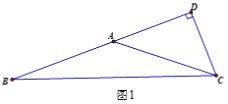
(2)如图2,过点B作BE∥AC交DC延长线于点E,连接AE交BC于点G.若∠DCB=2∠CAE+∠ABC,求证:∠AEB=∠AEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
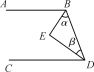
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
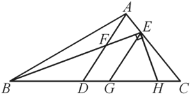
【题目】如图,在△ABC中,已知∠ABC=30°,点D在BC上,点E在AC上,∠BAD=∠EBC, AD交BE于F.
(1)求∠BFD的度数;
(2)若EG∥AD交BC于G,EH⊥BE交BC于H,求∠HEG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com