
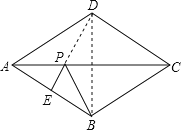
【题目】如图,菱形ABCD的周长为16,∠ADC=120,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是___________.

【答案】2![]()
【解析】
连接BD,根据菱形的对角线平分一组对角可得∠BDA=![]() ∠ADC=60°,然后判断出△ABD是等边三角形,连接DE,根据轴对称确定最短路线问题,DE与AC的交点即为所求的点P,PE+PB的最小值=DE,然后根据等边三角形的性质求出DE即可得解.
∠ADC=60°,然后判断出△ABD是等边三角形,连接DE,根据轴对称确定最短路线问题,DE与AC的交点即为所求的点P,PE+PB的最小值=DE,然后根据等边三角形的性质求出DE即可得解.
解:如图,连接BD,
∵四边形ABCD是菱形,
∴∠BDA=![]() ∠ADC=
∠ADC=![]() ×120°=60°,
×120°=60°,
∵AB=AD(菱形的邻边相等),
∴△ABD是等边三角形,
连接DE,∵B、D关于对角线AC对称,
∴DE与AC的交点即为所求的点P,PE+PB的最小值=DE,
∵E是AB的中点,
∴DE⊥AB,
∵菱形ABCD周长为16,
∴AD=16÷4=4,
∴DE=![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
(1)如图1,若MP⊥CD,则∠BMP=___度;
(2)如图2,当P点在CD延长线上时,∠BMP=___(用α表示);
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求下列事件的概率:
(1)两次取的小球的标号相同
(2)两次取的小球的标号的和等于4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:
作物种类 | 每公顷所需人数/人 | 每公顷投入资金/万元 |
蔬菜 | 4 | 2 |
水果 | 5 | 3 |
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
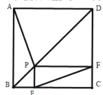
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=2EC.其中正确的结论是___________________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)平移后的三个顶点坐标分别为:.A1( ),B1( ),C1( ).
(2)在上图中画出平移后三角形A1B1C1;
(3)画出△AOA1并求出△AOA1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
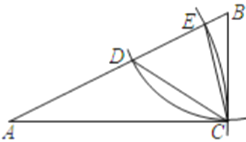
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求![]() 的度数.
的度数.
(2)设![]() .
.
①线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根吗?说明理由.
的一个根吗?说明理由.
②若![]() 为
为![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点. 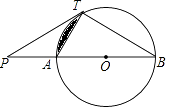
(1)求证:PT2=PAPB;
(2)若PT=TB= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com