
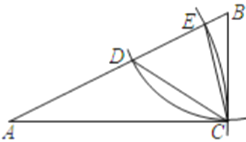
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求![]() 的度数.
的度数.
(2)设![]() .
.
①线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根吗?说明理由.
的一个根吗?说明理由.
②若![]() 为
为![]() 的中点,求
的中点,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的周长为16,∠ADC=120,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1) ①依题意补全图形;
②求证:BE⊥AC.
(2)请探究线段BE,AD,CN所满足的等量关系,并证明你的结论.
(3)设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为______________(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]() +(b﹣3)2=0,(c﹣4)2≤0.
+(b﹣3)2=0,(c﹣4)2≤0.

(1) a=_____、b=_____、c=_____;
(2)求四边形AOBC的面积;
(3)如果在第二象限内有一点P(m,![]() ),且四边形ABOP的面积与△ABC的面积相等 ,求出点P的坐标.
),且四边形ABOP的面积与△ABC的面积相等 ,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E. 
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com