
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]() +(b﹣3)2=0,(c﹣4)2≤0.
+(b﹣3)2=0,(c﹣4)2≤0.

(1) a=_____、b=_____、c=_____;
(2)求四边形AOBC的面积;
(3)如果在第二象限内有一点P(m,![]() ),且四边形ABOP的面积与△ABC的面积相等 ,求出点P的坐标.
),且四边形ABOP的面积与△ABC的面积相等 ,求出点P的坐标.
【答案】(1)a=2,b=3,c=4; (2)9; (3)P(-3,![]() )
)
【解析】
(1)根据二次根式和平方的非负性可得结论;
(2)根据四边形AOBC的面积=△AOB的面积+△ABC的面积计算即可;
(3)根据P和A、B的坐标,由S四边形ABOP=S△AOP+S△AOB得出四边形ABOP的面积;根据四边形ABOP的面积与△ABC的面积相等,列式可得m=﹣3,从而得P的坐标.
(1)∵![]() (b﹣3)2=0,(c﹣4)2≤0,∴a﹣2=0,b﹣3=0,c﹣4=0,∴a=2,b=3,c=4;
(b﹣3)2=0,(c﹣4)2≤0,∴a﹣2=0,b﹣3=0,c﹣4=0,∴a=2,b=3,c=4;
(2)四边形AOBC的面积=△AOB的面积+△ABC的面积=![]() =3+6=9;
=3+6=9;
(3)由(1)知:OA=2,OB=3,∴S四边形ABOP=S△AOP+S△AOB![]() AO|xP|
AO|xP|![]() AOOB=﹣m
AOOB=﹣m![]() m+3.
m+3.
∵B(3,0),C(3,4),∴BC⊥x轴,∴S△ABC![]() BCxB
BCxB![]() 4×3=6,∴﹣m+3=6,m=﹣3,则当m=﹣3时,四边形ABOP的面积与△ABC的面积相等,此时P(﹣3,
4×3=6,∴﹣m+3=6,m=﹣3,则当m=﹣3时,四边形ABOP的面积与△ABC的面积相等,此时P(﹣3,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
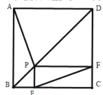
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=2EC.其中正确的结论是___________________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
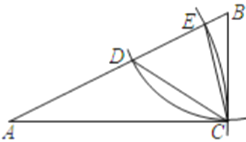
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求![]() 的度数.
的度数.
(2)设![]() .
.
①线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根吗?说明理由.
的一个根吗?说明理由.
②若![]() 为
为![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com