
【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
【答案】(1)见解析;(2)三;(3)120户
【解析】
(1)根据月用电量是0<x≤5的户数是6,对应的频率是0.12,求出调查的总户数,然后利用总户数乘以频率就是频数,频数除以总数就是频率,即可得出答案;再根据求出的频数,即可补全统计图;
(2)根据中位数的定义结合各组的频数可得结果;
(3)根据表格求出月均用水量在20<x≤25的频率,进而求出月均用水量超过20t的频率,乘以1000即可得到结果.
解:(1)调查的家庭总数是:6÷0.12=50(户),
则月用水量5<x≤10的频数是:50×0.24=12(户),
月用水量20<x≤25的频率=![]() =0.08;
=0.08;
故答案为:12,0.08;
补全的图形如下图:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| 12 | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | 0.08 |
| 2 | 0.04 |
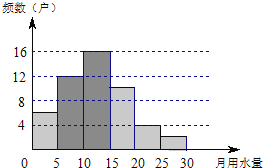
(2)∵各组的频数分别为6,12,16,10,4,2,
∴月均用水量的中位数落在第三小组;
(3)月均用水量在20<x≤25的频率为1-(0.12+0.24+0.32+0.20+0.04)=0.08,
故月均用水量超过20t的频率为0.08+0.04=0.12,
则该小区月均用水量超过20t的家庭大约有1000×0.12=120(户).


科目:初中数学 来源: 题型:
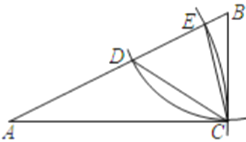
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交线段
长为半径画弧,交线段![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求![]() 的度数.
的度数.
(2)设![]() .
.
①线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的一个根吗?说明理由.
的一个根吗?说明理由.
②若![]() 为
为![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点. 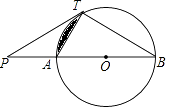
(1)求证:PT2=PAPB;
(2)若PT=TB= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小; 
(2)如图②,当BE=BC时,求∠CDO的大小. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F. 
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1 , △A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2 .
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2 , 请写出点P1、P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
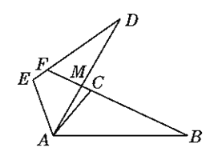
【题目】如图,已知△ABC≌△ADE,BC的延长线交AD于点M,交DE于点F.若∠D=25°,∠AED=105°,∠DAC=10°,求∠DFB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com