
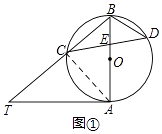
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小; 
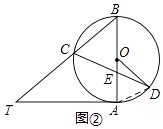
(2)如图②,当BE=BC时,求∠CDO的大小. 
【答案】
(1)解:如图①,∵连接AC,
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°﹣∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°﹣∠ABC=40°,
∴∠CDB=∠CAB=40°;
(2)解:如图②,连接AD,
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA﹣∠ADC=65°﹣50°=15°.
【解析】(1)根据切线的性质:圆的切线垂直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;(2)如图②,连接AD,根据等边对等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1) ①依题意补全图形;
②求证:BE⊥AC.
(2)请探究线段BE,AD,CN所满足的等量关系,并证明你的结论.
(3)设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为______________(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,存在直线![]() 和直线
和直线![]() .
.
(1)直接写出![]() 两点的坐标;
两点的坐标;
(2)求出直线![]() 、直线
、直线![]() 的交点
的交点![]() 及两条直线与
及两条直线与![]() 轴围成的三角形的面积;
轴围成的三角形的面积;
(3)结合图象,直接写出![]() 时
时![]() 的取值范围_______.
的取值范围_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF. 
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G. 
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角,(本题中所有角都是指大于0°且小于180°的角)
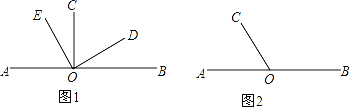
(1)如图1所示,O为直线AB上一点,OC⊥AB,OE⊥OD,图中哪些角互为垂角?(写出所有情况)
(2)如图2所示,O为直线AB上一点,∠AOC=60°,将∠AOC绕点O顺时针旋转n°(0°<n<120),OA旋转得到OA′,OC旋转得到OC′,当n为何值时,∠AOC′与∠BOA′互为垂角?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形向右平移3个单位长度,再向上平移2个单位长度,则平移后三个顶点的坐标为( )
A.(-1,-1),(2,3),(5,1)
B.(-1,1),(3,2),(5,1)
C.(-1,1),(2,3),(5,1)
D.(1,-1),(2,2),(5,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米∕秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:

(1)平移到1.5秒时,重叠部分的面积为 厘米2.
(2)求小正方形在平移过程中,S与t的关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com