
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.
A.4
B.3
C.2
D.1
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)如图1,△ABC和△E中,AB=CB,DB=EB,∠ABC=∠DBE=90°,D点在AB上,连接AE、DC.则AE和CD有什么数量和位置关系? 
(2)类比: 若将图1中的△DBE绕点B逆时针旋转一个锐角,如图2所示,问图2中的线段AE,CD之间的数量和位置关系还成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为( )
A.50°
B.60°
C.150°
D.50°或130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.

问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=40°,∠C=50°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( ) 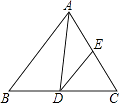
A.40°
B.45°
C.50°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了 ![]() (为非负整数)的展开式的项数及各项系数的有关规律.
(为非负整数)的展开式的项数及各项系数的有关规律.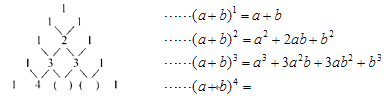
(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+4ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过 ![]() 天是星期 .
天是星期 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com